
【题目】如图,在四棱柱ABCD﹣A1B1C1D1中,侧棱A1A⊥底面ABCD,AB⊥AC,AB=1,AC=AA1=2,AD=CD= ![]() .用向量法解决下列问题:
.用向量法解决下列问题: 
(1)若AC的中点为E,求A1C与DE所成的角;
(2)求二面角B1﹣AC﹣D1(锐角)的余弦值.
【答案】
(1)解:由AD=CD,AC的中点为E,∴DE⊥AC.
如图,以A为原点,AB为x轴,AC为y轴,AA1为z轴,建立空间直角坐标系,
依题意可得A(0,0,0 ),B(1,0,0),A1(0,0,2)
C(0,2,0),D(﹣2,1,0),B1(1,0,2),
D1(﹣2,1,2),E(0,1,0).
![]() =(0,2,﹣2),
=(0,2,﹣2), ![]() =(2,0,0),
=(2,0,0),
∵ ![]()
![]() =0,∴A1C⊥DE,
=0,∴A1C⊥DE,
∴A1C与DE所成的角为 ![]() .
.
(2)解:设平面B1AC与平面D1AC所成的角为θ,
平面B1AC的法向量为 ![]() =(x,y,1),平面D1AC的法向量为
=(x,y,1),平面D1AC的法向量为 ![]() =(a,b,1).
=(a,b,1).
![]() =(﹣1,0,﹣2),
=(﹣1,0,﹣2), ![]() =(2,﹣1,﹣2),
=(2,﹣1,﹣2), ![]() =(0,2,0).
=(0,2,0).
由 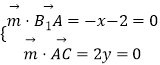 ,得
,得 ![]() =(﹣2,0,1),
=(﹣2,0,1),
由 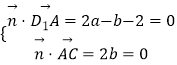 ,得
,得 ![]() =(1,0,1),
=(1,0,1),
则cosθ= ![]() =
= ![]() =
= ![]() ,
,
∴二面角B1﹣AC﹣D1(锐角)的余弦值为 ![]() .
.
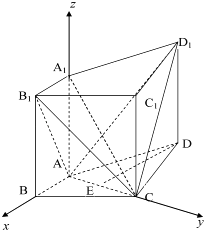
【解析】(1)以A为原点,AB为x轴,AC为y轴,AA1为z轴,建立空间直角坐标系,利用向量法能求出A1C与DE所成的角.(2)求出平面B1AC的法向量和平面D1AC的法向量,利用向量法能求出二面角B1﹣AC﹣D1(锐角)的余弦值.
【考点精析】解答此题的关键在于理解异面直线及其所成的角的相关知识,掌握异面直线所成角的求法:1、平移法:在异面直线中的一条直线中选择一特殊点,作另一条的平行线;2、补形法:把空间图形补成熟悉的或完整的几何体,如正方体、平行六面体、长方体等,其目的在于容易发现两条异面直线间的关系.


科目:高中数学 来源: 题型:
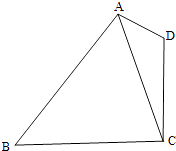
【题目】如图,在平面四边形ABCD中,AD=1,CD=2,AC= ![]() .
. 
(1)求cos∠CAD的值;
(2)若cos∠BAD=﹣ ![]() ,sin∠CBA=
,sin∠CBA= ![]() ,求BC的长.
,求BC的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线y2=ax上一点M(4,b)到焦点的距离为6.
(1)求抛物线的方程;
(2)若此抛物线与直线y=kx﹣2交于不同的两点A、B,且AB中点的横坐标为2,求k的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直三棱柱ABC﹣A1B1C1中,AB=AC=5,BB1=BC=6,D,E分别是AA1和B1C的中点 
(1)求证:DE∥平面ABC;
(2)求三棱锥E﹣BCD的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知双曲线 ![]() (a>0,b>0)的两条渐近线与抛物线D:y2=2px(p>0)的准线分别交于A,B两点,O为坐标原点,双曲线的离心率为
(a>0,b>0)的两条渐近线与抛物线D:y2=2px(p>0)的准线分别交于A,B两点,O为坐标原点,双曲线的离心率为 ![]() ,△ABO的面积为2
,△ABO的面积为2 ![]() .
.
(1)求双曲线C的渐近线方程;
(2)求p的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知△ABC的三个顶点坐标分别为A(﹣1,1),B(7,﹣1),C(﹣2,5),AB边上的中线所在直线为l.
(1)求直线l的方程;
(2)若点A关于直线l的对称点为D,求△BCD的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】盒子中有5个大小形状完全相同的小球,其中黑色小球有3个,标号分别为1,2,3,白色小球有2个,标号分别为1,2.
(1)若从盒中任取两个小球,求取出的小球颜色相同且标号之和小于或等于4的概率;
(2)若盒子里再放入一个标号为4的红色小球,从中任取两个小球,求取出的两个小球颜色不同且标号之和大于3的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】样本(x1 , x2…,xn)的平均数为x,样本(y1 , y2 , …,ym)的平均数为 ![]() (
( ![]() ≠
≠ ![]() ).若样本(x1 , x2…,xn , y1 , y2 , …,ym)的平均数
).若样本(x1 , x2…,xn , y1 , y2 , …,ym)的平均数 ![]() =α
=α ![]() +(1﹣α)
+(1﹣α) ![]() ,其中0<α<
,其中0<α< ![]() ,则n,m的大小关系为( )
,则n,m的大小关系为( )
A.n<m
B.n>m
C.n=m
D.不能确定
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com