
分析 根据函数的定义域范围由内往外依次代入计算可得.
解答 解:由题意:函数f(x)=$\left\{\begin{array}{l}{{2}^{x}-1,(x≤0)}\\{lo{g}_{2}x+1(x>0)}\end{array}\right.$
∵$\frac{1}{4}>0$
f($\frac{1}{4}$)=$lo{g}_{2}\frac{1}{4}+1$=-1.
则f(f($\frac{1}{4}$))=f(-1);
又∵-1<0,
f(-1)=2-1-1=-$\frac{1}{2}$,
∴得f(f($\frac{1}{4}$))=$-\frac{1}{2}$.
故答案为$-\frac{1}{2}$.
点评 本题考查了复合函数的带值计算问题.属于基础题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
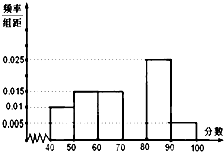 某校高二年级共1000人,从参加期末数学考试的学生中抽出20名学生,将其成绩(均为整数)分成六段[40,50),[50,60)…[90,100],然后画出如图所示频率分布直方图,但是缺失了第四组[70,80)的信息.观察图形的信息,回答下列问题.
某校高二年级共1000人,从参加期末数学考试的学生中抽出20名学生,将其成绩(均为整数)分成六段[40,50),[50,60)…[90,100],然后画出如图所示频率分布直方图,但是缺失了第四组[70,80)的信息.观察图形的信息,回答下列问题.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{5}}}{3}$ | B. | $-\frac{{\sqrt{5}}}{3}$ | C. | $\frac{{2\sqrt{5}}}{3}$ | D. | $-\frac{{2\sqrt{5}}}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com