练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    2．函数f（x）=x|x+a|+b是奇函数的充要条件是（　　）
    A．ab=0B．a+b=0C．a2+b2=0D．a=b

    分析 由奇函数的性质可得：f（0）=b=0，于是f（x）=x|x+a|，由f（-x）+f（x）=0，x≠0时，|x-a|=|x+a|恒成立，解得a=0．

    解答 解：由奇函数的性质可得：f（0）=b=0，
    ∴f（x）=x|x+a|，
    则f（-x）+f（x）=0，∴-x|-x+a|+x|x+a|=0，
    x≠0时，|x-a|=|x+a|恒成立，则a=0．
    ∴函数f（x）=x|x+a|+b是奇函数的充要条件是a=b=0，即a2+b2=0．
    故选：C．

    点评 本题考查了函数的奇偶性，考查了推理能力与计算能力，属于中档题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：2016-2017学年安徽六安一中高一上国庆作业二数学试卷（解析版） 题型：选择题

    已知函数的定义域为，值域为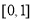，那么满足条件的整数对共有（ ）

    A．6个 B．7个

    C.8个 D．9个

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    13．已知椭圆C：$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1（a＞b＞0）的离心率为$\frac{{\sqrt{6}}}{3}$，上顶点为（0，1）．
    （Ⅰ）求椭圆C的方程；
    （Ⅱ）若过原点O作两条互相垂直的射线，与椭圆C交于A，B两点，求证：点O到直线AB的距离为定值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    10．随机变量ξ的分布列为：
    ξ0123
    Px0.20.30.4
    随机变量ξ的方差D（ξ）1．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    17．设函数y=f（x）的定义域为D，值域为A，如果存在函数x=g（t），使得函数y=f[g（t）]的值域仍是A，那么称x=g（t）是函数y=f（x）的一个等值域变换．设f（x）=log2x的定义域为[2，8]，已知x=g（t）=$\frac{{m{t^2}-nt+m}}{{{t^2}+1}}（{m∈R，n∈{R_+}}）$是y=f（x）的一个等值变换，且函数y=f[g（t）]的定义域为R，则m=5，n=6．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    7．函数f（x）=x3+ax2+3x-1在x=-3时取得极值，则a=（　　）
    A．2B．3C．4D．5

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    14．已知点A（1，0），B（0，1），C（2sinθ，cosθ）．
    （1）若|$\overrightarrow{AC}$|=|$\overrightarrow{BC}$|，求$\frac{sinθ+2cosθ}{sinθ-cosθ}$的值；
    （2）若（$\overrightarrow{OA}$+2$\overrightarrow{OB}$）•$\overrightarrow{OC}$=1，其中O为坐标原点，求sinθ•cosθ的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

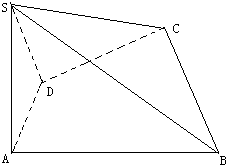    11．如图四棱锥S-ABCD，底面四边形ABCD满足条件∠DAB=90°，∠ADC=135°，AB=5，CD=2$\sqrt{2}$，AD=2，侧面SAD垂直于底面ABCD，SA=2，
    （1）若SB上存在一点E，使得CE∥平面SAD，求$\frac{SE}{SB}$的值；
    （2）求此四棱锥体积的最大值；
    （3）当体积最大时，求二面角A-SC-B大小的余弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    12．极坐标系中，圆心在$（1，\frac{π}{4}）$，半径为1的圆的方程为（　　）
    A．$ρ=2sin（θ-\frac{π}{4}）$B．$ρ=2cos（θ-\frac{π}{4}）$C．$ρcos（θ-\frac{π}{4}）=2$D．$ρsin（θ-\frac{π}{4}）=2$

    查看答案和解析>>

    同步练习册答案