
分析 (1)若|$\overrightarrow{AC}$|=|$\overrightarrow{BC}$|,则cosθ=2sinθ,代入可得$\frac{sinθ+2cosθ}{sinθ-cosθ}$的值;
(2)若($\overrightarrow{OA}$+2$\overrightarrow{OB}$)•$\overrightarrow{OC}$=1,则sinθ+cosθ=$\frac{1}{2}$,两边平方可得sinθ•cosθ的值.
解答 解:(1)∵A(1,0),B(0,1),C(2sinθ,cosθ).
∴$\overrightarrow{AC}$=(2sinθ-1,cosθ),
$\overrightarrow{BC}$=(2sinθ,cosθ-1),
若|$\overrightarrow{AC}$|=|$\overrightarrow{BC}$|,则(2sinθ-1)2+cos2θ=4sin2θ+(cosθ-1)2,
解得:cosθ=2sinθ,
∴$\frac{sinθ+2cosθ}{sinθ-cosθ}$=$\frac{sinθ+4sinθ}{sinθ-2sinθ}$=-5;
(2)若($\overrightarrow{OA}$+2$\overrightarrow{OB}$)•$\overrightarrow{OC}$=1,
则(1,2)•(2sinθ,cosθ)=2sinθ+2cosθ=1,
即sinθ+cosθ=$\frac{1}{2}$,
∴(sinθ+cosθ)2=1+2sinθ•cosθ=$\frac{1}{4}$,
∴sinθ•cosθ=-$\frac{3}{8}$.
点评 本题考查的知识点是平面向量的数量积运算,向量的模,三角函数的恒等变换,难度中档.


 科学实验活动册系列答案
科学实验活动册系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
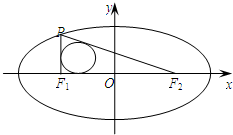 已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右焦点分别为F1、F2,焦距为4,且经过点(2,-3).若点P在椭圆上,且在x轴上方,$\overrightarrow{P{F}_{1}}$•$\overrightarrow{{F}_{1}{F}_{2}}$=0.
已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右焦点分别为F1、F2,焦距为4,且经过点(2,-3).若点P在椭圆上,且在x轴上方,$\overrightarrow{P{F}_{1}}$•$\overrightarrow{{F}_{1}{F}_{2}}$=0.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
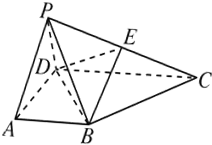 已知在四棱锥P-ABCD中,底面ABCD是直角梯形,∠BAD=90°,2AB=2AD=CD,侧面PAD是正三角形且垂直于底面ABCD,E是PC的中点.
已知在四棱锥P-ABCD中,底面ABCD是直角梯形,∠BAD=90°,2AB=2AD=CD,侧面PAD是正三角形且垂直于底面ABCD,E是PC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|{$\frac{3}{2}$<x<2} | B. | {x|${\frac{1}{2}$<x<2} | C. | {x|x<1} | D. | {x|-1<x<$\frac{3}{2}}\right.$} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com