
分析 (Ⅰ)由已知,求出a,b,c的值,可得椭圆的标准方程;
(Ⅱ)将直线的方程y=x+m与椭圆的方程4x2+y2=1联立,得到5x2+2mx+m2-1=0,利用△=-16m2+20≥0即可求得m的取值范围;
(Ⅲ)利用两点间的距离公式,再借助于韦达定理即可得到:两交点AB之间的距离|AB|=$\sqrt{2}$ $\sqrt{({x}_{1}+{x}_{2})^{2}-4{x}_{1}{x}_{2}}$=$\frac{2\sqrt{10}}{5}$,从而可求得m的值.
解答 (本小题满分10分)
解:(Ⅰ)∵椭圆中心在原点,焦点在y轴上,且过点A(0,1),离心率为$\frac{{\sqrt{3}}}{2}$,
∴a=1,$\frac{c}{a}$=$\frac{{\sqrt{3}}}{2}$,
∴c=$\frac{{\sqrt{3}}}{2}$,
∴b=$\frac{1}{2}$,
∴椭圆的标准方程为:${y}^{2}+\frac{{x}^{2}}{\frac{1}{4}}=1$,即4x2+y2=1:
(Ⅱ)把直线y=x+m代入椭圆方程得:4x2+(x+m)2=1
即:5x2+2mx+m2-1=0,
△=(2m)2-4×5×(m2-1)=-16m2+20≥0
解得:-$\frac{\sqrt{5}}{2}$≤m≤$\frac{\sqrt{5}}{2}$.
(Ⅲ)设该直线与椭圆相交于两点A(x1,y1),B(x2,y2),
则x1,x2是方程5x2+2mx+m2-1=0的两根,
由韦达定理可得:x1+x2=-$\frac{2m}{5}$,x1•x2=$\frac{{m}^{2}-1}{5}$,
∴|AB|=$\sqrt{2}$ $\sqrt{({x}_{1}+{x}_{2})^{2}-4{x}_{1}{x}_{2}}$=$\sqrt{2[(-\frac{2m}{5})^{2}-4×\frac{{m}^{2}-1}{5})}$=$\frac{2\sqrt{10}}{5}$;
∴m=0.
∴直线的方程为y=x.
点评 本题考查直线与圆锥曲线的位置关系与弦长问题,难点在于弦长公式的灵活应用,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $ρ=2sin(θ-\frac{π}{4})$ | B. | $ρ=2cos(θ-\frac{π}{4})$ | C. | $ρcos(θ-\frac{π}{4})=2$ | D. | $ρsin(θ-\frac{π}{4})=2$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
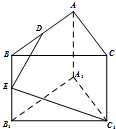 在正三棱柱ABC-A1B1C1中,AB=2,点D、E分别是棱AB、BB1的中点,若DE⊥EC1,则侧棱AA1的长为( )
在正三棱柱ABC-A1B1C1中,AB=2,点D、E分别是棱AB、BB1的中点,若DE⊥EC1,则侧棱AA1的长为( )| A. | 1 | B. | 2 | C. | $\sqrt{2}$ | D. | $2\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
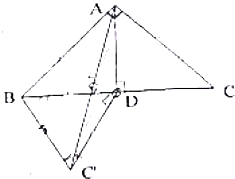 如图,在△ABC中,∠BAC=90°,AB=AC=2,AD⊥BC于D.将△ADC沿AD翻折至△ADC′,下列说法中正确的是①③④(写出所有正确命题的序号)
如图,在△ABC中,∠BAC=90°,AB=AC=2,AD⊥BC于D.将△ADC沿AD翻折至△ADC′,下列说法中正确的是①③④(写出所有正确命题的序号)查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | $\frac{1}{5}$ | C. | $\frac{1}{2}$ | D. | $\frac{1}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com