练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
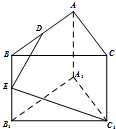
    19．在正三棱柱ABC-A1B1C1中，AB=2，点D、E分别是棱AB、BB1的中点，若DE⊥EC1，则侧棱AA1的长为（　　）
    A．1B．2C．$\sqrt{2}$D．$2\sqrt{2}$

    分析 设侧棱AA1的长为2x，则由题意，可得4+x2+1+x2=4x2+（2×$\frac{\sqrt{3}}{2}$ ）2，求出x，即可得出结论

    解答 解：取A1B1的中点D1，
    连接DD1，C1D1，DC1，

    设侧棱AA1的长为2x，
    则由题意，可得4+x2+1+x2=4x2+（2×$\frac{\sqrt{3}}{2}$ ）2，
    ∴x=1，2x=2．
    故选：B．

    点评 本题考查侧棱AA1的长的计算，考查勾股定理的运用，正确运用勾股定理是关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

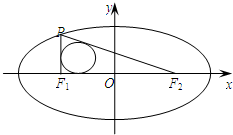    9．已知椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的左、右焦点分别为F1、F2，焦距为4，且经过点（2，-3）．若点P在椭圆上，且在x轴上方，$\overrightarrow{P{F}_{1}}$•$\overrightarrow{{F}_{1}{F}_{2}}$=0．
    （1）求椭圆C的方程；
    （2）①求△PF1F2的内切圆M的方程；
    ②若直线l过△PF1F2的内切圆圆心M，交椭圆于A，B两点，且A，B关于点M对称，求直线l的方程．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    10．在四棱锥P-ABCD中，底面ABCD为矩形，侧棱PD⊥底面ABCD，且$PD=CD=\frac{{\sqrt{2}}}{2}BC$，过棱PC的中点AB1⊥PQ，作EF⊥PB交PB于点PQD，连接DE，DF，BD，BE．
    （1）证明：PB⊥平面DEF．
    （2）求异面直线与BE所成角的余弦值及二面角B-DE-F的余弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    7．已知函数y=f（x）的图象关于原点对称，且当x∈（-∞，0），f（x）+xf′（x）＜0成立，若a=（-2）×f（-2），b=f（1），c=3×f（3），则a，b，c的关系大小是（　　）
    A．b＞a＞cB．c＞b＞aC．c＞a＞bD．a＞c＞b

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    14．关于x的方程2sinx-cos2x=m的解集是空集，则实数m的取值范围是（-∞，-2）∪（2，+∞）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    4．已知椭圆中心在原点，焦点在y轴上，且过点A（0，1），离心率为$\frac{{\sqrt{3}}}{2}$，设直线方程为y=x+m．
    （Ⅰ）求椭圆标准方程
    （Ⅱ）当m为何值时，直线与椭圆有公共点？
    （Ⅲ）若直线被椭圆截得的弦长为$\frac{2\sqrt{10}}{5}$，求直线的方程．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    11．对于函数f（x），若存在实数M＞0，使得对于定义域内的任意的x，使得函数|f（x）|≤M，则称函数f（x）为有界函数，下列函数是有界函数的是④⑤⑥
    ①y=2x+1
    ②y=-x2+2x
    ③y=2x-1
    ④y=lnx（x∈（1，e]）
    ⑤y=2-|x|
    ⑥$y=\frac{x}{|x|+2}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    8．一个多面体的三视图如图所示，则此多面体的表面积是（　　）
    A．10B．12C．8+4$\sqrt{2}$D．12+4$\sqrt{2}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    9．已知P为椭圆$\frac{x^2}{36}+\frac{y^2}{9}=1$上的任意一点，O为坐标原点，M在线段OP上，且$\overrightarrow{OM}=\frac{1}{3}\overrightarrow{OP}$
    （1）求点M的轨迹E的方程；
    （2）若A（-4，0），B（0，4），C为轨迹E上的动点，求△ABC面积的最大值．

    查看答案和解析>>

    同步练习册答案