
| A. | b>a>c | B. | c>b>a | C. | c>a>b | D. | a>c>b |
分析 构造函数F(x)=xf(x),求导数,判断单调性求解,再判断F(x)的奇偶性,即可得到F(-3)>F(-2)>F(-1),问题得以解决.
解答 解:令函数F(x)=xf(x),则F′(x)=f(x)+xf′(x)
∵f(x)+xf′(x)<0,
∴F(x)=xf(x)在(-∞,0)单调递减,
∵函数y=f(x)的图象关于原点对称,
∴y=f(x)是定义在R上的奇函数,
可知F(x)=xf(x)在R上为偶函数
∵a=-2f(-2),b=f(1),c=3•f(3),
∴a=F(-2),b=F(-1),c=F(-3)
∴F(-3)>F(-2)>F(-1),
即c>a>b
故选:C
点评 本题考察了复合函数的求导,导数在单调性中的应用,关键构造函数,掌握函数的奇偶性和单调性,属于中档题


 同步练习强化拓展系列答案
同步练习强化拓展系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
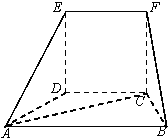 在如图的几何体中,四边形CDEF为正方形,四边形ABCD为等腰梯形,AB∥CD,AB=2BC,∠ABC=60°,AC⊥FB.
在如图的几何体中,四边形CDEF为正方形,四边形ABCD为等腰梯形,AB∥CD,AB=2BC,∠ABC=60°,AC⊥FB.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $ρ=2sin(θ-\frac{π}{4})$ | B. | $ρ=2cos(θ-\frac{π}{4})$ | C. | $ρcos(θ-\frac{π}{4})=2$ | D. | $ρsin(θ-\frac{π}{4})=2$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
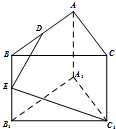 在正三棱柱ABC-A1B1C1中,AB=2,点D、E分别是棱AB、BB1的中点,若DE⊥EC1,则侧棱AA1的长为( )
在正三棱柱ABC-A1B1C1中,AB=2,点D、E分别是棱AB、BB1的中点,若DE⊥EC1,则侧棱AA1的长为( )| A. | 1 | B. | 2 | C. | $\sqrt{2}$ | D. | $2\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | $\frac{1}{5}$ | C. | $\frac{1}{2}$ | D. | $\frac{1}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
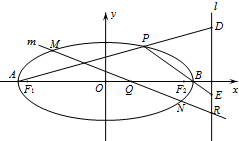 椭圆C的方程为$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),F1,F2分别是它的左、右焦点,已知椭圆C过点(0,1),且离心率e=$\frac{2\sqrt{2}}{3}$.
椭圆C的方程为$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),F1,F2分别是它的左、右焦点,已知椭圆C过点(0,1),且离心率e=$\frac{2\sqrt{2}}{3}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com