解:(1)由题意得,m>8-m>0,解得4<m<8,
所以实数m的取值范围是(4,8);
(2)因为m=6,所以椭圆C的方程为

,
①设点P坐标为(x,y),则

,
因为点M的坐标为(1,0),
所以PM
2=(x-1)
2+y
2=

=

=

,

,
所以当x=

时,PM的最小值为

,此时对应的点P坐标为(

);
②由a
2=6,b
2=2,得c
2=4,即c=2,
从而椭圆C的右焦点F的坐标为(2,0),右准线方程为x=3,离心率e=

,
设A(x
1,y
1),B(x
2,y
2),AB的中点H(x
0,y
0),
则

,

,
两式相减得,

,即

,
令k=k
AB,则线段AB的垂直平分线l的方程为y-y
0=-

(x-x
0),
令y=0,则x
N=ky
0+x
0=

,
因为F(2,0),所以FN=|x
N-2|=

,
因为AB=AF+BF=e(3-x
1)+e(3-x
2)=

|x
0-3|.
故
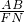
=

=

,即
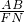
为定值

.
分析:(1)由焦点在x轴上得,m>8-m>0,解出即可;
(2)①设点P坐标为(x,y),则

,由两点间距离公式可表示出PM
2,根据二次函数的性质即可求得PM
2的最小值,从而得到PM的最小值,注意x的取值范围;②易求焦点F的坐标及右准线方程,设A(x
1,y
1),B(x
2,y
2),AB的中点H(x
0,y
0),利用平方差法可用H坐标表示直线AB的斜率,用点斜式写出AB中垂线方程,从而得点N横坐标,进而得到线段FN的长,由第二定义可表示出线段AB长,
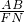
是定值可证;
点评:本题考查直线与圆锥曲线的位置关系、椭圆方程的求解及椭圆的第二定义,考查学生综合运用知识分析解决问题的能力,属中档题.

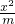 +
+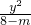 =1.
=1.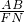 是定值,并求出这个定值.
是定值,并求出这个定值. ,
, ,
, =
= =
= ,
, ,
, 时,PM的最小值为
时,PM的最小值为 ,此时对应的点P坐标为(
,此时对应的点P坐标为( );
); ,
, ,
, ,
, ,即
,即 ,
, (x-x0),
(x-x0), ,
, ,
, |x0-3|.
|x0-3|.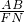 =
= =
= ,即
,即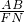 为定值
为定值 .
. ,由两点间距离公式可表示出PM2,根据二次函数的性质即可求得PM2的最小值,从而得到PM的最小值,注意x的取值范围;②易求焦点F的坐标及右准线方程,设A(x1,y1),B(x2,y2),AB的中点H(x0,y0),利用平方差法可用H坐标表示直线AB的斜率,用点斜式写出AB中垂线方程,从而得点N横坐标,进而得到线段FN的长,由第二定义可表示出线段AB长,
,由两点间距离公式可表示出PM2,根据二次函数的性质即可求得PM2的最小值,从而得到PM的最小值,注意x的取值范围;②易求焦点F的坐标及右准线方程,设A(x1,y1),B(x2,y2),AB的中点H(x0,y0),利用平方差法可用H坐标表示直线AB的斜率,用点斜式写出AB中垂线方程,从而得点N横坐标,进而得到线段FN的长,由第二定义可表示出线段AB长,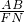 是定值可证;
是定值可证;

 如图,在平面直角坐标系xOy中,锐角α和钝角β的终边分别与单位圆交于A,B两点.
如图,在平面直角坐标系xOy中,锐角α和钝角β的终边分别与单位圆交于A,B两点.