
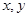 (
(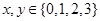 ),满足
),满足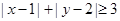 电脑显示“中奖”,且抽奖者获得特等奖奖金;否则电脑显示“谢谢”,则不中奖。
电脑显示“中奖”,且抽奖者获得特等奖奖金;否则电脑显示“谢谢”,则不中奖。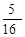 (2)a≤9900
(2)a≤9900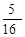 .
.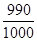 ,P(ξ=900)=
,P(ξ=900)=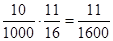 ,P(ξ="a)="
,P(ξ="a)=" 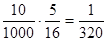 .
.| ξ | -100 | 900 | a |
| P | 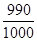 |  | 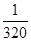 |
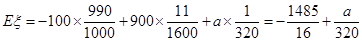 .
.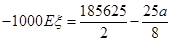 ,
,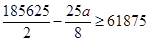 ,解得a≤9900.
,解得a≤9900.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
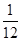 ,
,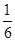 ,
,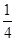 ,
,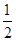 .游戏规则如下:
.游戏规则如下: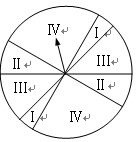
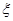 .
.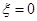 的概率;
的概率;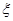 的概率分布及数学期望.
的概率分布及数学期望.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
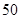 名职工休年假的次数进行的调查统计结果如下表所示:
名职工休年假的次数进行的调查统计结果如下表所示:| 休假次数 |  | 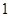 | 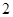 | 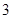 |
| 人数 | 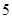 |  | 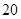 | 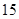 |
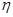 表示这两人休年假次数之和,记“函数
表示这两人休年假次数之和,记“函数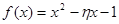 ,在区间
,在区间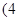 ,
,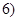 上有且只有一个零点”为事件
上有且只有一个零点”为事件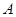 ,求事件
,求事件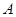 发生的概率
发生的概率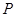 ;
;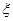 表示这两人休年假次数之差的绝对值,求随机变量
表示这两人休年假次数之差的绝对值,求随机变量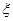 的分布列及数学期望
的分布列及数学期望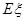 .
.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 );
);查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com