
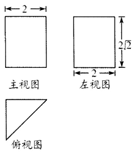
 《九章算术》中将底面是直角三角形的直三棱柱称之为“堑堵”,已知某“堑堵”的三视图如图所示,则该“堑堵”的外接球的表面积为16π.
《九章算术》中将底面是直角三角形的直三棱柱称之为“堑堵”,已知某“堑堵”的三视图如图所示,则该“堑堵”的外接球的表面积为16π. 分析 由已知可得该“堑堵”是一个以俯视图为底面的直三棱柱,求出棱柱外接球的半径,进而可得该“堑堵”的外接球的表面积.
解答 解:由已知可得该“堑堵”是一个以俯视图为底面的直三棱柱,
底面外接球的半径r=$\frac{\sqrt{{2}^{2}+{2}^{2}}}{2}$=$\sqrt{2}$,
球心到底面的距离d=$\frac{h}{2}$=$\sqrt{2}$,
故该“堑堵”的外接球的半径R=$\sqrt{{r}^{2}+{d}^{2}}$=2,
故该“堑堵”的外接球的表面积:S=4πR2=16π,
故答案为:16π
点评 本题考查的知识点是棱柱的体积和表面积,棱锥的体积和表面积,球的体积和表面积,简单几何体的三视图,难度基础.


科目:高中数学 来源: 题型:选择题
| A. | ①②④ | B. | ②③ | C. | ①③④ | D. | ②④ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
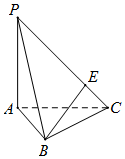 如图,在三棱锥P-ABC中,PA⊥平面ABC,AB=BC,PA=AC,E为PC上的动点,当 BE⊥PC时,$\frac{CE}{PC}$的值为$\frac{1}{4}$.
如图,在三棱锥P-ABC中,PA⊥平面ABC,AB=BC,PA=AC,E为PC上的动点,当 BE⊥PC时,$\frac{CE}{PC}$的值为$\frac{1}{4}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
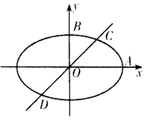 已知椭圆E:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率e=$\frac{\sqrt{3}}{2}$,且过点($\frac{\sqrt{3}}{2}$,$\frac{1}{4}$).
已知椭圆E:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率e=$\frac{\sqrt{3}}{2}$,且过点($\frac{\sqrt{3}}{2}$,$\frac{1}{4}$).查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | -1 | C. | $\sqrt{3}$ | D. | -$\sqrt{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com