
���� ����d����A��B���Ķ�����뼴�ɵó���
������A��x1��y1����B��x2��y2������d1��A��B��=|x1-x2|+|y1-y2|��${d_2}��A��B��={��{|{{x_1}-{x_2}}|^2}+{|{{y_1}-{y_2}}|^2}��^{\frac{1}{2}}}$��ͨ������չ������֤����
����D��?D�����Ӽ�����ȡ��x0��y0����D����${d_��}��M��O��={��{|{x_0}|^��}+{|{y_0}|^��}��^{\frac{1}{��}}}��1$����x0��y0�������ۣ�����֤����
��� ���⣺d1��A��B��=|1-2|+|1-3|=3��
d2��A��B��=$[|1-2{|}^{2}+|1-3{|}^{2}]^{\frac{1}{2}}$=${5}^{\frac{1}{2}}$=$\sqrt{5}$��
����֤������A��x1��y1����B��x2��y2������d1��A��B��=|x1-x2|+|y1-y2|��${d_2}��A��B��={��{|{{x_1}-{x_2}}|^2}+{|{{y_1}-{y_2}}|^2}��^{\frac{1}{2}}}$��
${d_1}^2��A��B��={��|{{x_1}-{x_2}}|+|{{y_1}-{y_2}}|��^2}$=${x_1}^2+{x_2}^2+{y_1}^2+{y_2}^2-2{x_1}{x_2}-2{y_1}{y_2}+2|{{x_1}-{x_2}}||{{y_1}-{y_2}}|$��
${d_2}^2��A��B��=��{|{{x_1}-{x_2}}|^2}+{|{{y_1}-{y_2}}|^2}��$=${x_1}^2+{x_2}^2+{y_1}^2+{y_2}^2-2{x_1}{x_2}-2{y_1}{y_2}$��
����d2��A��B����d1��A��B��������
��Ϊ${��\sqrt{2}{d_2}��A��B����^2}=2{x_1}^2+2{x_2}^2+2{y_1}^2+2{y_2}^2-4{x_1}{x_2}-4{y_1}{y_2}$��
����${��\sqrt{2}•{d_2}��A��B����^2}-{d_1}{��A��B��^2}$=${x_1}^2+{x_2}^2+{y_1}^2+{y_2}^2-2{x_1}{x_2}-2{y_1}{y_2}-2|{{x_1}-{x_2}}||{{y_1}-{y_2}}|$=${��{x_1}-{x_2}��^2}+{��{y_1}-{y_2}��^2}-2|{{x_1}-{x_2}}||{{y_1}-{y_2}}|$=${��|{x_1}-{x_2}|-|{y_1}-{y_2}|��^2}��0$��
����${d_1}��A��B����\sqrt{2}{d_2}��A��B��$������
����D��?D�����Ӽ���
֤�����£�
��ȡ��x0��y0����D����${d_��}��M��O��={��{|{x_0}|^��}+{|{y_0}|^��}��^{\frac{1}{��}}}��1$��
��x0=1��y0=0ʱ��d����M��O��=0��d����M��O��=0����ʱD��⊆D����
��|x0|=1��|y0|=0ʱ��${d_��}��M��O��={��{|{x_0}|^��}+{|{y_0}|^��}��^{\frac{1}{��}}}=1$��d����M��O��=1��
��ʱD��⊆D����
ͬ���ɵã���|x0|=0��|y0|=1ʱ��D��⊆D����
��|x0|��1��|y0|��1ʱ����Ϊ${d_��}��M��O��={��{|{x_0}|^��}+{|{y_0}|^��}��^{\frac{1}{��}}}��1$������ ${|{x_0}|^��}+{|{y_0}|^��}��1$��
����Ϊ0�������£�����${|{x_0}|^��}+{|{y_0}|^��}��{|{x_0}|^��}+{|{y_0}|^��}��1$����ʱD��⊆D����
��֮��������
����D��?D����
���� ���⿼�����¶��塢����֮��Ĺ�ϵ������֮��ľ��빫ʽ���������۷���������ʽ�Ľⷨ����������������������������������⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����

| A�� | 16 | B�� | 19 | C�� | 20 | D�� | 38 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 54 | B�� | 72 | C�� | 78 | D�� | 96 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | �ཻ | B�� | ���� | C�� | ���� | D�� | �ں� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
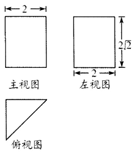 �������������н�������ֱ�������ε�ֱ��������֮Ϊ��ǵ�¡�����֪ij��ǵ�¡�������ͼ��ͼ��ʾ����á�ǵ�¡��������ı����Ϊ16�У�
�������������н�������ֱ�������ε�ֱ��������֮Ϊ��ǵ�¡�����֪ij��ǵ�¡�������ͼ��ͼ��ʾ����á�ǵ�¡��������ı����Ϊ16�У��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 2x+y-3=0 | B�� | x+y-3=0 | C�� | x-y-1=0 | D�� | 2x-y-5=0 |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com