
【题目】海水养殖场进行某水产品的新、旧网箱养殖方法的产量对比,收获时各随机抽取了100个网箱,测量各箱水产品的产量(单位:![]() )得频率分布直方图如下:
)得频率分布直方图如下:


(1)设两种养殖方法的箱产量相互独立,记![]() 表示事件:“旧养殖法的箱产量低于
表示事件:“旧养殖法的箱产量低于![]() ,新养殖法的箱产量不低于
,新养殖法的箱产量不低于![]() ”,估计
”,估计![]() 的概率;
的概率;
(2)填写下面![]() 列联表,并根据联表判断是否有
列联表,并根据联表判断是否有![]() 的把握认为箱产量与养殖方法有关:
的把握认为箱产量与养殖方法有关:
箱产量 | 箱产量 | |
旧养殖法 | ||
新养殖法 |
附:
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
(3)根据箱产量的频率分布直方图,求新养殖法箱产量的中位数的估计值(精确到0.01)
【答案】(1)![]() (2)填表见解析,有
(2)填表见解析,有![]() 的把握认为箱产量与养殖方法有关(3)
的把握认为箱产量与养殖方法有关(3)![]()
【解析】
(1)利用独立事件概率公式求得事件![]() 的概率估计值;
的概率估计值;
(2)写出列联表计算![]() ,得到答案.
,得到答案.
(3)结合频率分布直方图估计中位数计算得到答案..
(1)记![]() 表示事件“旧养殖法的箱产量低于
表示事件“旧养殖法的箱产量低于![]() ”,
”,![]() 表示事件“新养殖法的箱产量不低于
表示事件“新养殖法的箱产量不低于![]() ”,由题意知
”,由题意知![]() ,
,
旧养殖法的箱产量低于![]() 的频率为
的频率为![]() ,故
,故![]() 的估计值为0.62.
的估计值为0.62.
新养殖法的箱产量不低于![]() 的频率为
的频率为![]() ,
,
故![]() 的估计值为0.66.
的估计值为0.66.
因此事件![]() 的概率估计值为
的概率估计值为![]() .
.
(2)根据箱产量的频率分布直方图得列联表
箱产量 | 箱产量 | |
旧养殖法 | 62 | 38 |
新养殖法 | 34 | 66 |
![]() .
.
由于![]() ,故有
,故有![]() 的把握认为箱产量与养殖方法有关.
的把握认为箱产量与养殖方法有关.
(3)因为新养殖法的箱产量频率分布直方图中,箱产量低于![]() 的直方图面积为
的直方图面积为
![]() ,
,
箱产量低于![]() 的直方图面积为
的直方图面积为![]() ,
,
故新养殖法箱产量的中位数的估计值为![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】某商店为了解气温对某产品销售量的影响,随机记录了该商店![]() 月份中
月份中![]() 天的日销售量
天的日销售量![]() (单位:千克)与该地当日最低气温
(单位:千克)与该地当日最低气温![]() (单位:℃)的数据,如表所示:
(单位:℃)的数据,如表所示:
|
|
|
|
|
|
|
|
|
|
|
|
(1)求![]() 与
与![]() 的回归方程
的回归方程![]() :
:
(2)判断![]() 与
与![]() 之间是正相关还是负相关;若该地
之间是正相关还是负相关;若该地![]() 月份某天的最低气温为
月份某天的最低气温为![]() ,请用(1)中的回归方程预测该商店当日的销售量.
,请用(1)中的回归方程预测该商店当日的销售量.
参考公式: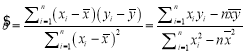 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义在![]() 上的函数
上的函数![]() 满足:
满足:![]() 对任意的实数
对任意的实数![]() 都成立,当且仅当
都成立,当且仅当![]() 时取等号,则称函数
时取等号,则称函数![]() 是
是![]() 上的
上的![]() 函数,已知
函数,已知![]() 函数
函数![]() 具有性质:
具有性质:![]() (
(![]() ,
,![]() )对任意的实数
)对任意的实数![]() (
(![]() )都成立,当且仅当
)都成立,当且仅当![]() 时取等号.
时取等号.
(1)试判断函数![]() (
(![]() 且
且![]() )是否是
)是否是![]() 上的
上的![]() 函数,说明理由;
函数,说明理由;
(2)求证:![]() 是
是![]() 上的
上的![]() 函数,并求
函数,并求![]() 的最大值(其中
的最大值(其中![]() 、
、![]() 、
、![]() 是△
是△![]() 三个内角);
三个内角);
(3)若![]() 定义域为
定义域为![]() ,
,
① ![]() 是奇函数,证明:
是奇函数,证明:![]() 不是
不是![]() 上的
上的![]() 函数;
函数;
② ![]() 最小正周期为
最小正周期为![]() ,证明:
,证明:![]() 不是
不是![]() 上的
上的![]() 函数.
函数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某运动队从![]() 四位运动员中选拔一人参加某项赛事,在选拔结果公布前,甲、乙、丙、丁四位教练对这四位运动员预测如下:甲说:“是
四位运动员中选拔一人参加某项赛事,在选拔结果公布前,甲、乙、丙、丁四位教练对这四位运动员预测如下:甲说:“是![]() 或
或![]() 被选中”; 乙说:“是
被选中”; 乙说:“是![]() 被选中”;丙说:“
被选中”;丙说:“![]() ,
,![]() 均未被选中”; 丁说:“是
均未被选中”; 丁说:“是![]() 被选中”.若这四位教练中只有两位说的话是对的,则获得参赛资格的运动员是____.
被选中”.若这四位教练中只有两位说的话是对的,则获得参赛资格的运动员是____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com