已知f(x)是定义在(-∞,0)∪(0,+∞)上的奇函数,当x∈(0,+∞)时,f(x)=ax+2lnx,(a∈R)
(1)求f(x)的解析式;
(2)是否存在负实数a,使得当x∈[-e,0)时,f(x)的最小值是4?如果存在,求出a的值;如果不存在,请说明理由.
(3)对x∈D如果函数F(x)的图象在函数G(x)的图象的下方,则称函数F(x)在D上被函数G(x)覆盖.求证:若a=1时,函数f(x)在区间x∈(1,+∞)上被函数g(x)=x3覆盖.
【答案】
分析:(1)已知x∈(0,+∞)时,f(x)=ax+2lnx,可以令x<0,得-x>0,代入f(x)即可求解;
(2)假设存在,已知当x∈(0,+∞)时,f(x)=ax+2lnx,对f(x)进行求导,利用导数求出x∈[-e,0)的最小值让其等于4,求出a值,从而进行判断;
(3)由题意要证函数f(x)在区间x∈(1,+∞)上被函数g(x)=x
3覆盖等价于需证x
3>x+2lnx对x∈(1,+∞)恒成立,然后令h(x)=x
3-x-2lnx(x>1),求出其导数会发现h(x)为单调增函数,可知f(x)在(1,+∞)上的最小值为h(1),从而求证;
解答:解:(1)当x∈(-∞,0),则-x>0,由已知得,
f(-x)=-ax+2ln(-x)=-f(x),
∴f(x)=ax-2ln(-x),
∴
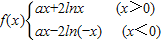
;
(2)假设存在a<0,满足题意,∵f(x)=ax-2ln(-x),x∈[-∞,0)
∴f′(x)=a+
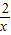
=
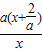
,x∈[-∞,0),
令f′(x)=0,x=-
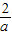
,
当-
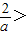
-e,即a<
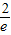
时,f(x)在(-e,-
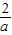
)是减函数,在(-
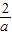
,0)为增函数,
∴f(x)
min=f(-
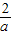
)=4,解得a=-2e,
当-
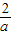
≤-e,即0>a≥
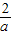
时,f(x)在(-e,0)上增函数,
∴f(x)
min=f(-e)=4,解得a=-
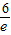
<-
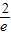
矛盾;
综上所诉,存在a=-2e满足题意.
(3)证明:由题意知,只需证x
3>x+2lnx对x∈(1,+∞)恒成立,
令h(x)=x
3-x-2lnx(x>1),
∴h′(x)=3x
2-1-
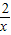
=
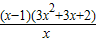
,
∵x>1,∴x-1>0,3x
2+3x+2>0,
∴h′(x)>0,对x∈(1,+∞)恒成立,
∴x>1时,h(x)>h(1)=0
∴h(x)>0?x
3>x+2lnx对x∈(1,+∞)恒成立,即证;
点评:第一问利用函数的奇偶性进行求解,比较常见,第三问是一道证明题,定义了一个新定义覆盖的概念,将这个问题转化为函数的恒成立的问题,就会比较简单;

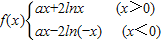 ;
;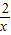 =
=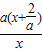 ,x∈[-∞,0),
,x∈[-∞,0),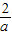 ,
,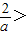 -e,即a<
-e,即a<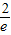 时,f(x)在(-e,-
时,f(x)在(-e,-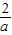 )是减函数,在(-
)是减函数,在(-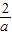 ,0)为增函数,
,0)为增函数,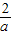 )=4,解得a=-2e,
)=4,解得a=-2e,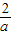 ≤-e,即0>a≥
≤-e,即0>a≥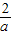 时,f(x)在(-e,0)上增函数,
时,f(x)在(-e,0)上增函数,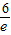 <-
<-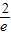 矛盾;
矛盾;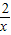 =
=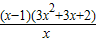 ,
,

 阅读快车系列答案
阅读快车系列答案