
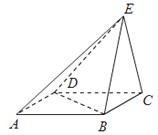
【题目】如图,![]() 是平行四边形,已知
是平行四边形,已知![]() ,
,![]() ,平面
,平面![]() 平面
平面![]() .
.
(1)证明:![]() ;
;
(2)若![]() ,求平面
,求平面![]() 与平面
与平面![]() 所成二面角的平面角的余弦值.
所成二面角的平面角的余弦值.
【答案】(1)见解析;(2)![]() .
.
【解析】
(1)推导出![]() ,取BC的中点F,连结EF ,可推出
,取BC的中点F,连结EF ,可推出![]() ,从而
,从而![]() 平面
平面![]() ,进而
,进而![]() ,由此得到
,由此得到![]() 平面
平面![]() ,从而
,从而![]() ;(2)以
;(2)以![]() 为坐标原点,
为坐标原点,![]() ,
,![]() 所在直线分别为
所在直线分别为![]() ,
,![]() 轴,以过点
轴,以过点![]() 且与
且与![]() 平行的直线为
平行的直线为![]() 轴,建立空间直角坐标系,利用向量法能求出平面
轴,建立空间直角坐标系,利用向量法能求出平面![]() 与平面
与平面![]() 所成二面角的余弦值.
所成二面角的余弦值.
(1)∵![]() 是平行四边形,且
是平行四边形,且![]()
∴![]() ,故
,故![]() ,即
,即![]()
取BC的中点F,连结EF.
∵![]()
∴![]()
又∵平面![]() 平面
平面![]()
∴![]() 平面
平面![]()
∵![]() 平面
平面![]()
∴![]()
∵![]() 平面
平面![]()
∴![]() 平面
平面![]() ,
,
∵![]() 平面
平面![]()
∴![]()
(2)∵![]() ,由(Ⅰ)得
,由(Ⅰ)得![]()
以![]() 为坐标原点,
为坐标原点,![]() 所在直线分别为
所在直线分别为![]() 轴,建立空间直角坐标系(如图),则
轴,建立空间直角坐标系(如图),则![]()
∴![]()
设平面![]() 的法向量为
的法向量为![]() ,则
,则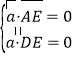 ,即
,即![]()
得平面![]() 的一个法向量为
的一个法向量为![]()
由(1)知![]() 平面
平面![]() ,所以可设平面
,所以可设平面![]() 的法向量为
的法向量为![]()
设平面![]() 与平面
与平面![]() 所成二面角的平面角为
所成二面角的平面角为![]() ,则
,则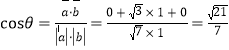
即平面![]() 与平面
与平面![]() 所成二面角的平面角的余弦值为
所成二面角的平面角的余弦值为![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】已知等差数列{an}的前n项和为Sn , 若Sm﹣1=﹣4,Sm=0,Sm+2=14(m≥2,且m∈N*).
(1)求m的值;
(2)若数列{bn}满足 ![]() =logabn(n∈N*),求数列{(an+6)bn}的前n项和.
=logabn(n∈N*),求数列{(an+6)bn}的前n项和.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】圆锥的轴截面SAB是边长为2的等边三角形,O为底面中心,M为SO的中点,动点P在圆锥底面内(包括圆周).若AM⊥MP,则P点形成的轨迹的长度为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了了解甲、乙两名同学的数学学习情况,对他们的![]() 次数学测试成绩(满分
次数学测试成绩(满分![]() 分)进行统计,作出如下的茎叶图,其中
分)进行统计,作出如下的茎叶图,其中![]() 处的数字模糊不清,已知甲同学成绩的中位数是
处的数字模糊不清,已知甲同学成绩的中位数是![]() ,乙同学成绩的平均分是
,乙同学成绩的平均分是![]() 分.
分.

(1)求![]() 和
和![]() 的值;
的值;
(2)现从成绩在![]() 之间的试卷中随机抽取两份进行分析,求恰抽到一份甲同学试卷的概率.
之间的试卷中随机抽取两份进行分析,求恰抽到一份甲同学试卷的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国古代名著《九章算术》中有这样一段话:“今有金锤,长五尺,斩本一尺,重四斤.斩末一尺,重二斤.”意思是:“现有一根金锤,头部的1尺,重4斤;尾部的1尺,重2斤;且从头到尾,每一尺的重量构成等差数列.”则下列说法错误的是( )
A.该金锤中间一尺重3斤
B.中间三尺的重量和是头尾两尺重量和的3倍
C.该金锤的重量为15斤
D.该金锤相邻两尺的重量之差的绝对值为0.5斤
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知全集U=R,A={y|y=2x+1},B={x|lnx<0},则(UA)∩B=( )
A.?
B.{x| ![]() <x≤1}
<x≤1}
C.{x|x<1}
D.{x|0<x<1}
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com