�⣺��1����f��-x��+f��x��=2x
2��2|x|�Ľ⼯ΪΪ[-1��1]
����������D=[-1��1]ֵ�� A=

��
��2����������[0��x
0]����ȡx
1��x
2����x
1��x
2����g��x
1����g��x
2��
��

��3t��x
12+x
22+x
1x
2��3x
02 ��
ͬ�� ����[x
0��1]�ϵ���������3t��3x
02���� 3t=3x
02��x
0�ʣ�0��1����t�ʣ�0��1����
��3�������� �ɣ�2���ĵ����Է���ͬ���ɵ� t �IJ�ͬȡֵ������g��x���ĵ�����
�ٵ� t��0ʱ������ g��x��=x
3-3tx+�� x��[0��1]������������B=[��
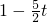
]��
��
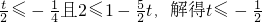
����
�ڵ� 0��t��1 ʱ������ g��x���ļ�����Ϊ��

��g��x������������[

��1]��
g��x���� x=�ﵽ��Сֵ��
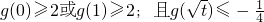
����0��t��1ì�ܣ� ��
�۵�t��1ʱ������ g��x�� ������[0��1]�����ݼ�����B=[
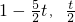
]
��
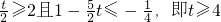
����������t��ȡֵ��Χ�ǣ�
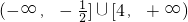
��
��4�����ģ� ����3����������
�� t��0ʱ������ g��x��=x
3-3tx+�� x��[0��1]������������B=[��
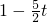
]��
��
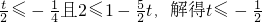
��
��5�����ģ� ��� ��2�������� ��t��1 ��
��������1����f��-x��+f��x��=2x
2��2|x|�Ľ⼯ΪΪ[-1��1]������������D��϶��κ��������ʿ���ֵ��A
��2����������[0��x
0]����ȡx
1��x
2����x
1��x
2����g��x
1����g��x
2���ɵ�3t��x
12+x
22+x
1x
2��3x
02 ͬ�� ����[x
0��1]�ϵ���������3t��3x
02�� 3t=3x
02��x
0�ʣ�0��1������t�ķ�Χ
��3�������� �ɣ�2���ĵ����Է���ͬ���ɵ� t �IJ�ͬȡֵ������g��x���ĵ�����
�ٵ� t��0ʱ������ g��x��=x
3-3tx+�� x��[0��1]��������������B����������t�ķ�Χ
�ڵ� 0��t��1 ʱ������ g��x���ļ�����Ϊ��

��g��x������������[

��1]��
g��x���� x=�ﵽ��Сֵ���۵�t��1ʱ������ g��x�� ������[0��1]�����ݼ�����t�ķ�Χ
��4�����ģ� ����3�������� �ٵ� t��0ʱ������ g��x��=x
3-3tx+�� x��[0��1]��������������B����������t�ķ�Χ
��5�����ģ� ��� ��2����������[0��x
0]����ȡx
1��x
2����x
1��x
2����g��x
1����g��x
2���ɵ�3t��x
12+x
22+x
1x
2��3x
02 ͬ�� ����[x
0��1]�ϵ���������3t��3x
02�� 3t=3x
02��x
0�ʣ�0��1������t�ķ�Χ
������������Ҫ�����˾���ֵ����ʽ�Ľⷨ�������κ����������ϵ���ֵ����⣬�����ĵ����Ե�Ӧ�ã������Ҫ�����߱���ǿ���������������������������

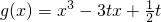 �Ķ�����Ϊ[0��1]��ֵ��ΪB��
�Ķ�����Ϊ[0��1]��ֵ��ΪB��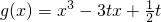 ��[0��x0]�ϵ����ݼ�����[x0��1]�ϵ�����������ʵ��t��ȡֵ��Χ����t��ʾx0��
��[0��x0]�ϵ����ݼ�����[x0��1]�ϵ�����������ʵ��t��ȡֵ��Χ����t��ʾx0��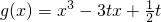 �ڶ�����[0��1]�ϵ����ݼ�����ʵ��t��ȡֵ��Χ��
�ڶ�����[0��1]�ϵ����ݼ�����ʵ��t��ȡֵ��Χ�� ��
��
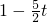 ]��
]��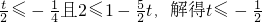 ����
���� ��g��x������������[
��g��x������������[ ��1]��
��1]��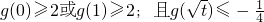 ����0��t��1ì�ܣ� ��
����0��t��1ì�ܣ� ��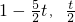 ]
]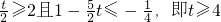
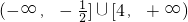 ��
��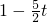 ]��
]��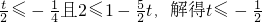 ��
�� ��g��x������������[
��g��x������������[ ��1]��
��1]��

 â���̸������Ծ�ϵ�д�
â���̸������Ծ�ϵ�д�