
| A. | $\sqrt{3}$ | B. | $\sqrt{2}$ | C. | $\frac{{\sqrt{3}}}{2}$ | D. | $\frac{{\sqrt{2}}}{2}$ |
分析 利用${V}_{A-{B}_{1}{C}_{1}E}$=${V}_{{C}_{1}-A{B}_{1}E}$,求出点C1到平面AB1E的距离.
解答 解:由题意,△AB1E中,B1E=AE=$\sqrt{5}$,AB1=2$\sqrt{2}$,∴${S}_{△A{B}_{1}E}$=$\frac{1}{2}×2\sqrt{2}×\sqrt{5-2}$=$\sqrt{6}$,
∵${S}_{△{B}_{1}{C}_{1}E}$=$\frac{1}{2}×2×1$=1,
∴${V}_{A-{B}_{1}{C}_{1}E}$=$\frac{1}{3}×1×\sqrt{3}$=$\frac{\sqrt{3}}{3}$,
设点C1到平面AB1E的距离为h,则${V}_{A-{B}_{1}{C}_{1}E}$=${V}_{{C}_{1}-A{B}_{1}E}$=$\frac{1}{3}×\sqrt{6}×h$=$\frac{\sqrt{3}}{3}$,
∴h=$\frac{\sqrt{2}}{2}$.
故选:D.
点评 本题考查点到面的距离的计算,考查三棱锥体积的计算,正确求出三棱锥的体积是关键.


科目:高中数学 来源: 题型:选择题
| A. | p,q,r都不大于2 | B. | p,q,r都不小于2 | ||
| C. | p,q,r至少有一个不小于2 | D. | p,q,r至少有一个不大于2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,-4] | B. | [-2,+∞) | C. | [-4,-2] | D. | (-∞,-4]∪[-2,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题

查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
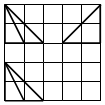 如图,网格纸上小正方形的边长为l,粗线画出的是某多面体的三视图,则该几何体的各个面中最大面的面积为( )
如图,网格纸上小正方形的边长为l,粗线画出的是某多面体的三视图,则该几何体的各个面中最大面的面积为( )| A. | l | B. | 2 | C. | 2$\sqrt{3}$ | D. | 4$\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
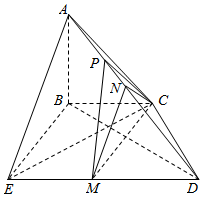 如图所示,平面ABC⊥平面BCDE,BC∥DE,$BC=\frac{1}{2}DE=2$,BE=CD=2,AB⊥BC,M,N分别为DE,AD中点.
如图所示,平面ABC⊥平面BCDE,BC∥DE,$BC=\frac{1}{2}DE=2$,BE=CD=2,AB⊥BC,M,N分别为DE,AD中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图,在多面体ABC-DEFG中,平面ABC∥平面DEFG,AC∥GF,且△ABC是边长为2的正三角形,DEFG是边长为4的正方形,M,N分别是AD,BE的中点,则MN=( )
如图,在多面体ABC-DEFG中,平面ABC∥平面DEFG,AC∥GF,且△ABC是边长为2的正三角形,DEFG是边长为4的正方形,M,N分别是AD,BE的中点,则MN=( )| A. | $\sqrt{7}$ | B. | 4 | C. | $\sqrt{19}$ | D. | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图所示为某几何体的三视图,其中正视图和左视图都是腰长为1的等腰直角三角形,该几何体的体积为V1,其外接球的体积为V2,则$\frac{{V}_{2}}{{V}_{1}}$的值为( )
如图所示为某几何体的三视图,其中正视图和左视图都是腰长为1的等腰直角三角形,该几何体的体积为V1,其外接球的体积为V2,则$\frac{{V}_{2}}{{V}_{1}}$的值为( )| A. | $\sqrt{3}$π | B. | 2$\sqrt{3}$π | C. | 3$\sqrt{3}$π | D. | $\frac{3\sqrt{3}π}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com