练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

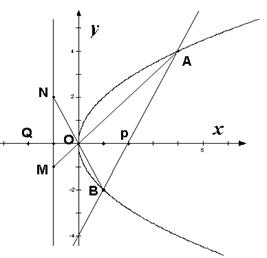
    （08年温州市适应性测试二理）  （14分） 如图，已知抛物线C：，为其准线，过其对称轴上一点P 作直线与抛物线交于A、B两点，连结OA、OB并延长AO、BO分别交于点M、N。

    （1）求的值;

    （2）记点Q是点P关于原点的对称点，设P分有向线段所成的比为，且

    求证： 

     

    解析：（1）证明：设

               由 ……………2分

               则  …………….…4分

               

               

               ……………7分

               

                                                         ……………9分

         

                

                                                          ……………14分

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    （08年温州市适应性测试二文）（14分）如图，点是点在平面上的射影，　

    是正三角形，且．

    （I）证明：四边形是正方形；

    （II）求与平面所成角的大小．

     

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （08年温州市适应性测试二文）（15分）已知函数在处取到极值，其中

    ．

    （I）若，求的值；

    （II）若，证明：过原点且与曲线相切的两条直线不垂直．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （08年温州市适应性测试二理） （15分）已知函数

    （1）求的单调区间；

    （2）对于给定的闭区间，试证明在（0,1）上必存在实数，使时，在

    上是增函数；

    （3）当时，记，若对于任意的总存在

    时，使得成立，求的最小值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （08年温州市适应性测试二理）  （15分）已知数列{}的前项的和为,对一切正整数都有

    （1）求证:是等差数列;并求数列{}的通项公式;

    （2）当,证明:

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （08年温州市适应性测试二理） （14分）一个袋子装有两个红球、两个白球，从袋子中任取两个球放入一箱子里，记 为箱子中红球的个数.再“从箱子里任取一个球，看看是红的还是白的，然后放回”，这样从箱子中反复取球两次.设表示红球被取出的次数.

    （1）求=1的概率

    （2）求的分布列与期望.

    查看答案和解析>>

    同步练习册答案