
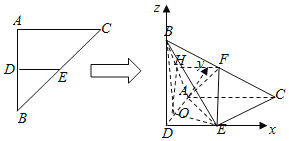
【题目】在等腰Rt△ABC中,∠BAC=90°,腰长为2,D、E分别是边AB、BC的中点,将△BDE沿DE翻折,得到四棱锥B﹣ADEC,且F为棱BC中点,BA![]() .
.
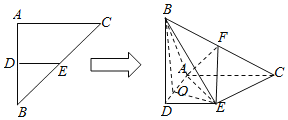
(1)求证:EF⊥平面BAC;
(2)在线段AD上是否存在一点Q,使得AF∥平面BEQ?若存在,求二面角Q﹣BE﹣A的余弦值,若不存在,请说明理由.
【答案】(1)证明见解析;(2)存在,![]()
【解析】
(1)取![]() 中点
中点![]() ,连结
,连结![]() 、
、![]() ,在等腰
,在等腰![]() 中,由已知可得
中,由已知可得![]() ,则
,则![]() ,由线面垂直的判定可得
,由线面垂直的判定可得![]() 平面
平面![]() ,进一步得到
,进一步得到![]() 平面
平面![]() ,则
,则![]() ,可得
,可得![]() 平面
平面![]() ,然后证明
,然后证明![]() 是平行四边形,得
是平行四边形,得![]() ,从而得到
,从而得到![]() 平面
平面![]() ;(2)以
;(2)以![]() 为原点建立如图所示空间直角坐标系
为原点建立如图所示空间直角坐标系![]() .求出
.求出![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 的坐标,设
的坐标,设![]() ,
,![]() ,
,![]() ,求出平面
,求出平面![]() 的法向量
的法向量![]() ,由
,由![]() 求得
求得![]() ,即线段
,即线段![]() 上存在一点
上存在一点![]() ,使得
,使得![]() 平面
平面![]() ,再求出平面
,再求出平面![]() 的法向量为
的法向量为![]() ,由两法向量所成角的余弦值可得二面角
,由两法向量所成角的余弦值可得二面角![]() 的余弦值.
的余弦值.
(1)证明:取![]() 中点
中点![]() ,连结
,连结![]() 、
、![]() ,在等腰
,在等腰![]() 中,
中,
![]() ,
,![]() ,
,![]() 、
、![]() 分别是边
分别是边![]() 、
、![]() 的中点,
的中点,![]() ,
,
又![]() 翻折后
翻折后![]() ,
,![]() 翻折后
翻折后![]() ,且
,且![]() 为等腰直角三角形,则
为等腰直角三角形,则![]() ,
,
![]() 翻折后
翻折后![]() ,
,![]() ,且
,且![]() ,
,![]() 平面
平面![]() ,
,
![]() ,
,![]() 平面
平面![]() ,则
,则![]() ,
,
又![]() ,
,![]() 平面
平面![]() ,
,
又![]() ,
,![]() ,且
,且![]() ,
,
![]() 是平行四边形,则
是平行四边形,则![]() ,
,
![]() 平面
平面![]() ;
;
(2)以![]() 为原点建立如图所示空间直角坐标系
为原点建立如图所示空间直角坐标系![]() .则
.则![]() ,1,
,1,![]() ,
,![]() ,0,
,0,![]() ,
,![]() ,0,
,0,![]() ,
,![]() ,1,
,1,![]() ,
,![]() ,设
,设![]() ,
,![]() ,
,![]() ,
,
则![]() ,
,
设平面![]() 的法向量为
的法向量为![]() ,
,![]() ,
,![]() ,则由
,则由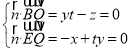 ,取
,取![]() ,则
,则![]() ,1,
,1,![]() ,
,
要使![]() 平面
平面![]() ,则须
,则须![]() ,
,
![]()
![]() ,即线段
,即线段![]() 上存在一点
上存在一点![]() ,使得
,使得![]() 平面
平面![]() ,
,
设平面![]() 的法向量为
的法向量为![]() ,
,![]() ,
,![]() ,则由
,则由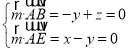 ,取
,取![]() ,则
,则![]() ,1,
,1,![]() ,
,
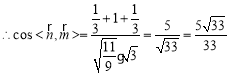 ,
,
![]() 二面角
二面角![]() 为锐二面角,
为锐二面角,![]() 其余弦值为
其余弦值为![]() ,
,
即线段![]() 上存在一点
上存在一点![]() (点
(点![]() 是线段
是线段![]() 上的靠近点
上的靠近点![]() 的一个三等分点),
的一个三等分点),
使得![]() 平面
平面![]() ,此时二面角
,此时二面角![]() 的余弦值为
的余弦值为![]() .
.


科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,圆
中,圆![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以直角坐标系的原点
为参数),以直角坐标系的原点![]() 为极点,
为极点,![]() 轴正半轴为极轴建立极坐标系.
轴正半轴为极轴建立极坐标系.
(1)求圆![]() 的极坐标方程;
的极坐标方程;
(2)设曲线![]() 的极坐标方程为
的极坐标方程为![]() ,曲线
,曲线![]() 的极坐标方程为
的极坐标方程为![]() ,求三条曲线
,求三条曲线![]() ,
,![]() ,
,![]() 所围成图形的面积.
所围成图形的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,M是椭圆C的上顶点,
,M是椭圆C的上顶点,![]() ,F2是椭圆C的焦点,
,F2是椭圆C的焦点,![]() 的周长是6.
的周长是6.
(Ⅰ)求椭圆C的标准方程;
(Ⅱ)过动点P(1,t)作直线交椭圆C于A,B两点,且|PA|=|PB|,过P作直线l,使l与直线AB垂直,证明:直线l恒过定点,并求此定点的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题正确的是( )
A.“若x=3,则x2﹣2x﹣3=0”的否命题是:“若x=3,则x2﹣2x﹣3≠0”
B.在△ABC中,“A>B”是“sinA>sinB”的充要条件
C.若p∧q为假命题,则p∨q一定为假命题
D.“存在x0∈R,使得ex0≤0”的否定是:不存在x0∈R,使得e![]() 0”
0”
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点Q是圆![]() 上的动点,点
上的动点,点![]() ,若线段QN的垂直平分线MQ于点P.
,若线段QN的垂直平分线MQ于点P.
(I)求动点P的轨迹E的方程
(II)若A是轨迹E的左顶点,过点D(-3,8)的直线l与轨迹E交于B,C两点,求证:直线AB、AC的斜率之和为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知常数![]() ,数列
,数列![]() 的前
的前![]() 项和为
项和为![]() ,
, ![]() ,
, ![]() ;
;
(1)求数列![]() 的通项公式;
的通项公式;
(2)若![]() ,且
,且![]() 是单调递增数列,求实数
是单调递增数列,求实数![]() 的取值范围;
的取值范围;
(3)若![]() ,
, ![]() ,对于任意给定的正整数
,对于任意给定的正整数![]() ,是否存在正整数
,是否存在正整数![]() 、
、![]() ,使得
,使得![]() ?若存在,求出
?若存在,求出![]() 、
、![]() 的值(只要写出一组即可);若不存在,请说明理由;
的值(只要写出一组即可);若不存在,请说明理由;
查看答案和解析>>
科目:高中数学 来源: 题型:
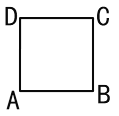
【题目】某人设计一项单人游戏,规则如下:先将一棋子放在如图所示正方形![]() (边长为2个单位)的顶点
(边长为2个单位)的顶点![]() 处,然后通过掷骰子来确定棋子沿正方形的边按逆时针方向行走了几个单位,如果掷出的点数为
处,然后通过掷骰子来确定棋子沿正方形的边按逆时针方向行走了几个单位,如果掷出的点数为![]() ,则棋子就按逆时针方向行走
,则棋子就按逆时针方向行走![]() 个单位,一直循环下去.则某人抛掷三次骰子后棋子恰好又回到起点
个单位,一直循环下去.则某人抛掷三次骰子后棋子恰好又回到起点![]() 处的所有不同走法共有( )
处的所有不同走法共有( )
A.21种B.22种C.25种D.27种
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,AE⊥平面ABCD,CF∥AE,AD∥BC,AD⊥AB,AB=AD=1,AE=BC=2.
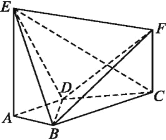
(1)求证:BF∥平面ADE;
(2)若二面角E-BD-F的余弦值为![]() ,求线段CF的长.
,求线段CF的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com