练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    试由
    1+tgx1-tgx
    =1+sin2x，求的x通值．
    分析：先根据正切函数与正余弦函数的关系将正切函数化为正余弦函数之比，然后再用二倍角公式和同角三角函数的基本关系进行整理化简，从而可得到2（cosx+sinx）•sin2x=0，最后根据三角函数的基本性质可求得x的值．
    解答：解：
    cosx+sinx
    cosx-sinx
    =(cosx+sinx)2
    （cosx+sinx）（1-cos2x+sin2x）=0
    2（cosx+sinx）•sin2x=0
    ∴cosx+sinx=0，即tgx=-1∴x=kπ-
    π
    4

    或sin2x=0∴x=kπ（k为整数）
    由检验可知，均为其通解．
    点评：本题主要考查同角三角函数的基本关系和二倍角公式的应用．考查对三角函数的基本知识和基本性质的运用，三角函数的知识点比较多，内容比较琐碎，一定要在平时注意多积累多练习．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：河北省衡水中学2011－2012学年高二下学期三调考试数学理科试题 题型：044

    某班一信息奥赛同学编了下列运算程序，将数据输入满足如下性质：

    ①输入1时，输出结果是；

    ②输入整数n(n≥2)时，输出结果f(n)是将前一结果f(n－1)先乘以3n－5，再除以3n＋1．

    (1)求f(2)，f(3)，f(4)；

    (2)试由(1)推测f(n)(其中n∈N*)的表达式，并给出证明．

    查看答案和解析>>

    科目：高中数学 来源： 题型：044

    当今世界进入了计算机时代，我们知道计算机装置有一个数据输入口A和一个运算结果的输出口B，某同学编入下列运算程序，将数据输入且满足以下性质：①从A输入1时，从B得到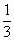．②从A输入整数n(n≥2)时，从B得到的结果f(n)是将前一结果f(n－1)先乘以奇数2n－3，再除以奇数2n＋1．

    (1)求f(2)，f(3)，f(4)；

    (2)试由(1)推测f(n)的表达式，并给出证明．

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

    试由
    1+tgx
    1-tgx
    =1+sin2x，求的x通值．

    查看答案和解析>>

    科目：高中数学 来源：1954年全国统一高考数学试卷（解析版） 题型：解答题

    试由=1+sin2x，求的x通值．

    查看答案和解析>>

    同步练习册答案