
| A. | 相交 | B. | 相离 | C. | 相切 | D. | 不确定 |
分析 将直线方程整理,可得该直线经过点M(-1,2),斜率为-m.再得到点M是圆内部的点,从而说明直线与圆相交.
解答 解:∵直线方程为mx+y+m-2=0,即y-2=-m(x+1)
∴该直线经过点M(-1,2),斜率为-m
又∵圆x2+y2-2x-9=0的圆心为C(1,0),半径r=$\sqrt{10}$
∴由|CM|=$\sqrt{4+4}$=2$\sqrt{2}$<r,得点M是圆x2+y2-2x-9=0内部的一点
∴直线mx+y+m-2=0与圆x2+y2-2x-9=0的位置关系是相交.
故选A.
点评 本题给出定圆与直线含有字母参数的方程,判断直线与圆的位置关系,着重考查了直线过定点、点与圆的位置关系和直线与圆的位置关系等知识,属于基础题.


 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案科目:高中数学 来源: 题型:选择题
| A. | {-2,0} | B. | {-4,-2,0} | C. | {4,6} | D. | {-4,-2,0,5} |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
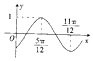 已知函数f(x)=sin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,则f($\frac{π}{2}$)的值为( )
已知函数f(x)=sin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,则f($\frac{π}{2}$)的值为( )| A. | -$\frac{\sqrt{3}}{2}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | -$\frac{\sqrt{3}}{3}$ | D. | $\frac{\sqrt{3}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,四棱锥S-ABCD中,SA=SD=BC,底面ABCD为正方形,且平面SAD⊥平面ABCD,M,N分别是AB,SC的中点.
如图,四棱锥S-ABCD中,SA=SD=BC,底面ABCD为正方形,且平面SAD⊥平面ABCD,M,N分别是AB,SC的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com