
某企业要建造一个容积为18m3,深为2m的长方体形无盖贮水池,如果池底和池壁每平方米的造价分别为200元和150元,怎样设计该水池可使得能总造价最低?最低总造价为多少?
将水池的地面设计成边长为3m的正方形时总造价最低,最低总造价为5400元.
【解析】
试题分析:
解题思路:设出未知量,根据容积为18,得出未知量间的关系,列出函数表达式,利用基本不等式进行求最值.
规律总结:解决数学应用题的步骤:①审题,设出有关量,注明自变量的取值范围;②列出函数表达式;③求函数的最值;④作答.
试题解析:设底面的长为xm,宽为ym,水池总造价为z元,
则由容积为18m3,可得:2xy=16,因此xy=9,
z=200×9+150(2×2x+2×2y)=1800+600(x+y)≥1800+600•2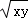 =5400
=5400
当且仅当x=y=3时,取等号.
所以,将水池的地面设计成边长为3m的正方形时总造价最低,最低总造价为5400元.
考点:基本不等式.


科目:高中数学 来源:2016届山西省高一5月月考数学试卷(解析版) 题型:选择题
函数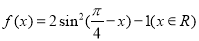 是( )
是( )
A.最小正周期为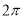 的奇函数 B.最小正周期为
的奇函数 B.最小正周期为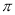 的奇函数
的奇函数
C.最小正周期为 的偶函数 D.最小正周期为
的偶函数 D.最小正周期为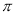 的偶函数
的偶函数
查看答案和解析>>
科目:高中数学 来源:2016届山西省高一下学期期中考试数学试卷(解析版) 题型:选择题
设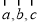 为非零向量,已知向量
为非零向量,已知向量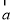 与
与 不共线,
不共线,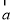 与
与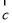 共线,则向量
共线,则向量 与
与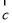 ( )
( )
A.一定不共线 B.一定共线 C.不一定共线 D.可能相等
查看答案和解析>>
科目:高中数学 来源:2016届山东省滨州市高一下学期期末考试数学试卷(解析版) 题型:选择题
把边长为1的正方形ABCD沿对角线BD折起,形成的三棱锥C﹣ABD的主视图与俯视图如图所示,则左视图的面积为( )
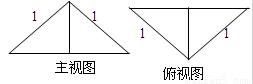
A.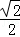 B.
B.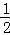 C.
C.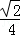 D.
D.
查看答案和解析>>
科目:高中数学 来源:2016届山东省济宁市高一下学期期中考试数学试卷(解析版) 题型:选择题
要得到函数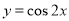 的图象,只需将
的图象,只需将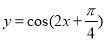 的图象( )
的图象( )
A.向左平移 个单位长度 B.向右平移
个单位长度 B.向右平移 个单位长度
个单位长度
C.向左平移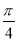 个单位长度 D.向右平移
个单位长度 D.向右平移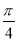 个单位长度
个单位长度
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com