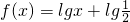Question

有下列四个命题：
（1）一定存在直线l使函数的图象与函数g（x）=lg（-x）+2的图象关于直线l对称
（2）不等式：arcsinx≤arccosx的解集为；
（3）已知数列{a_n}的前n项和为S_n=1-（-1）ⁿ，n∈N^*，则数列{a_n}一定是等比数列；
（4）过抛物线y²=2px（p＞0）上的任意一点M（x_°，y_°）的切线方程一定可以表示为y₀y=p（x+x₀）．
则正确命题的序号为________．

Answer 1

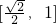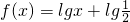解：（1）一定存在直线l使函数的图象与函数g（x）=lg（-x）+2的图象关于直线l对称，这是个错误命题，由于y=lgx与y=lg（-x）关于Y轴对称，但函数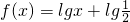的图象与函数g（x）=lg（-x）+2的图象向上平移的幅度不一样，故它们不关于y轴对称，由其图形结构知找不到这样的直线满足题意；
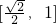（2）不等式：arcsinx≤arccosx的解集为是一个错误命题，因为自变量在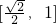时，arcsinx∈[，]，而arccosx∈[0，]故错误；
（3）已知数列{a_n}的前n项和为S_n=1-（-1）ⁿ，n∈N^*，则数列{a_n}一定是等比数列；，此命题正确，由于a_n=S_n-S_n-1=2×（-1）^n-1，当n=1时也成立，即数列的通项公式是2×（-1）^n-1，是一个等比数列．
（4）过抛物线y²=2px（p＞0）上的任意一点M（x_°，y_°）的切线方程一定可以表示为y₀y=p（x+x₀）是正确命题，由于直线y₀y=p（x+x₀）过点M（x_°，y_°），且与抛物线y²=2px（p＞0）有且只有一个交点，所以此命题正确
综上（3）（4）是正确命题，
故答案为（3）（4）
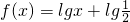分析：（1）一定存在直线l使函数的图象与函数g（x）=lg（-x）+2的图象关于直线l对称，可由对数函数的图象变换进行判断
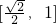（2）不等式：arcsinx≤arccosx的解集为，利用反三角函数的定义直接求解出符合条件的范围，解出解集；
（3）已知数列{a_n}的前n项和为S_n=1-（-1）ⁿ，n∈N^*，则数列{a_n}一定是等比数列，可求出其通项公式对它的性质进行研究判断其正误；
（4）过抛物线y²=2px（p＞0）上的任意一点M（x_°，y_°）的切线方程一定可以表示为y₀y=p（x+x₀），可通过解出其切数方程对比得出正误．
点评：本题考查命题的真真假判断，此类题一般涉及到的知识点较多，属于基础概念与基本方法考查题，解题的关键是理解每个命题所涉及的知识与方法，由此作出正确判断，此类题主要考查知识的记忆能力及利用知识判断推理的能力