
| AP |
| PB |

| AP |
| PB |
| λa |
| λ+1 |
| a |
| λ+1 |
| λa |
| λ+1 |
| a |
| λ+1 |
| a |
| λ+1 |
| λa |
| λ+1 |
| a |
| λ+1 |
| λa |
| λ+1 |
| λa |
| λ+1 |
| a |
| λ+1 |
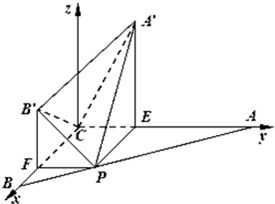
| CE |
| a |
| λ+1 |
| CB′ |
| λa |
| λ+1 |
| a |
| λ+1 |
| CB′ |
| CE |
| CA′ |
| a |
| λ+1 |
| λa |
| λ+1 |
| A′B′ |
| λa |
| λ+1 |
| a |
| λ+1 |
| (1-λ)a |
| λ+1 |
| B′P |
| a |
| λ+1 |
| a |
| λ+1 |
| m |
|
| m |
| 1 |
| λ |
| n |
| m |
| n |
| 1 |
| λ |


 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案科目:高中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| 6 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
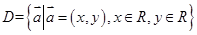 上也可以定义一个称“序”的关系,记为“
上也可以定义一个称“序”的关系,记为“ ”.定义如下:对于任意两个向量
”.定义如下:对于任意两个向量 当且仅当“
当且仅当“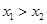 ”或“
”或“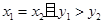 ”.按上述定义的关系“
”.按上述定义的关系“ ”,给出如下四个命题:
”,给出如下四个命题: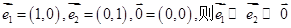 ;
;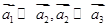 ,则
,则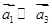 ;
;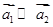 ,则对于任意
,则对于任意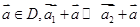 ;
;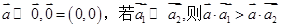 .
.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com