

 ,3-
,3- ),G(1+
),G(1+  ,3+
,3+  ); 设P点坐标为(x,x+2)(1-
); 设P点坐标为(x,x+2)(1-  <x<
<x< ),则Q(x,-x2+3x+4); ∴PQ=-x2+3x+4-x-2=-x2+2x+2; 易知M(
),则Q(x,-x2+3x+4); ∴PQ=-x2+3x+4-x-2=-x2+2x+2; 易知M(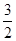 ,
,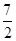 )。 若
)。 若 ,4-
,4-  ); ②以Q为直角顶点,PM为斜边;
); ②以Q为直角顶点,PM为斜边;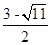 ,
,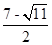 )故存在符合条件的P点,且P点坐标为(2-
)故存在符合条件的P点,且P点坐标为(2-  ,4-
,4-  )
)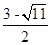 ,
,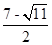 );(3)易知N(
);(3)易知N(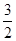 ,
,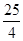 ),M(
),M(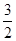 ,
,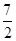 ); 设P点
); 设P点 <m<1+
<m<1+  ) ∴PQ=-m2+2m+2,
) ∴PQ=-m2+2m+2,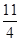 ; ①若四边形PMNQ是菱形,则首先四边形PMNQ是平行四边形,有: MN=PQ,
; ①若四边形PMNQ是菱形,则首先四边形PMNQ是平行四边形,有: MN=PQ,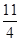 , 解得m=
, 解得m= 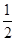 ,m=
,m= 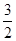 (舍去);当m=
(舍去);当m=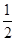 时,P(
时,P(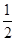 ,
,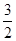 ),Q
),Q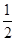 ,
, ) 此时PM≠MN,故四边形PMNQ不可能是菱形; ②由于当NQ∥PM时,
) 此时PM≠MN,故四边形PMNQ不可能是菱形; ②由于当NQ∥PM时,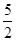 ,
,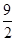 ).
).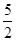 ,
,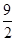 ).
).

 习题精选系列答案
习题精选系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com