
 数列{an}的各项排成如图所示的三角形形状,其中每一行比上一行增加两项,若
数列{an}的各项排成如图所示的三角形形状,其中每一行比上一行增加两项,若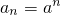 (a≠0),则位于第10行的第8列的项等于________,a2013在图中位于________.(填第几行的第几列)
(a≠0),则位于第10行的第8列的项等于________,a2013在图中位于________.(填第几行的第几列)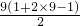 =81.
=81.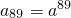 .
.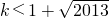 ,
,

科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源:江西省南昌市2011届高三第二次模拟考试数学理科试题 题型:044
将各项均为正数的数列{an}中的所有项按每一行比上一行多一项的规则排成数表,如图所示.记表中各行的第一个数a1,a2,a4,a7,…构成数列为{bn},各行的最后一个数a1,a3,a6,a10,…构成数列为{cn},第n行所有数的和为sn(n=1,2,3,4,…).已知数列{bn}是公差为d的等差数列,从第二行起,每一行中的数按照从左到右的顺序每一个数与它前面一个数的比是常数q,且a1=a13=1,a31=![]() .
.
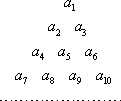
(1)求数列{cn},{sn}的通项公式.
(2)记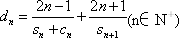 ,求证:
,求证: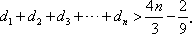 .
.
查看答案和解析>>
科目:高中数学 来源:江西省模拟题 题型:解答题
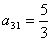 。
。
查看答案和解析>>
科目:高中数学 来源:《推理与证明》2013年广东省广州大学附中高考数学二轮复习检测(解析版) 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com