
如图,在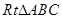 中,CD,CE分别是斜边AB上的高和中线,
中,CD,CE分别是斜边AB上的高和中线,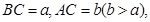
若t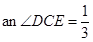 ,求
,求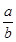 的值.
的值.

 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案科目:高中数学 来源: 题型:
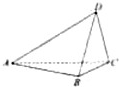 如图,在四面体ABCD中,平面ABC⊥平面ACD,AB⊥BC,AC=AD=2,BC=CD=1
如图,在四面体ABCD中,平面ABC⊥平面ACD,AB⊥BC,AC=AD=2,BC=CD=1查看答案和解析>>
科目:高中数学 来源: 题型:
 某先生居住在城镇的A处,准备开车到单位B处上班,若该地各路段发生堵车事件都是独立的,且在同一路段发生堵车事件最多只有一次,发生堵车事件的概率,如图.( 例如:A→C→D算作两个路段:路段AC发生堵车事件的概率为
某先生居住在城镇的A处,准备开车到单位B处上班,若该地各路段发生堵车事件都是独立的,且在同一路段发生堵车事件最多只有一次,发生堵车事件的概率,如图.( 例如:A→C→D算作两个路段:路段AC发生堵车事件的概率为| 1 |
| 10 |
| 1 |
| 15 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,在三棱锥A-BOC中,AO⊥面BOC,二面角B-AO-C是直二面角,OB=OC,∠OAB=
如图,在三棱锥A-BOC中,AO⊥面BOC,二面角B-AO-C是直二面角,OB=OC,∠OAB=| π | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:
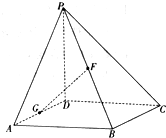 如图,在四棱锥P-ABCD中,PD⊥底面ABCD,底面ABCD为正方形,PD=DC=2,G、F分别是AD、PB的中点.
如图,在四棱锥P-ABCD中,PD⊥底面ABCD,底面ABCD为正方形,PD=DC=2,G、F分别是AD、PB的中点.查看答案和解析>>
科目:高中数学 来源: 题型:
 (2010•昆明模拟)如图,在正方形ABCD中,E、F分别是BC、CD的中点,AC∩EF=G.现在沿AE、EF、FA把这个正方形折成一个四面体,使B、C、D三点重合,重合后的点记为P,则在四面体P-AEF中必有( )
(2010•昆明模拟)如图,在正方形ABCD中,E、F分别是BC、CD的中点,AC∩EF=G.现在沿AE、EF、FA把这个正方形折成一个四面体,使B、C、D三点重合,重合后的点记为P,则在四面体P-AEF中必有( )查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com