练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    8．已知a${\;}^{\frac{1}{2}}$+a${\;}^{-\frac{1}{2}}$=2，求a+a-1，a2+a-2，a4+a-4的值．

    分析 a${\;}^{\frac{1}{2}}$+a${\;}^{-\frac{1}{2}}$=2，可得a+a-1=$（{a}^{\frac{1}{2}}+{a}^{-\frac{1}{2}}）^{2}$-2；a2+a-2=（a+a-1）2-2；a4+a-4=（a2+a-2）2-2．

    解答 解：∵a${\;}^{\frac{1}{2}}$+a${\;}^{-\frac{1}{2}}$=2，
    ∴a+a-1=$（{a}^{\frac{1}{2}}+{a}^{-\frac{1}{2}}）^{2}$-2=22-2=2；
    a2+a-2=（a+a-1）2-2=22-2=2；
    a4+a-4=（a2+a-2）2-2=22-2=2．

    点评 本题考查了乘法公式、指数幂的运算性质，考查了推理能力与计算能力，属于中档题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    18．若25a=53b=102c．试求a、b、c之间的关系．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

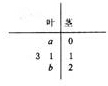    19．如图所示是某组数据的茎叶图，已知该组数据的平均数为$\frac{23}{2}$，ab=1（a，b∈R），则$\frac{a}{2}sin2x+bco{s}^{2}x-\frac{b}{2}$的最大值为$\frac{\sqrt{2}}{2}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    16．若集合A={0，1}，B={-1，1}，则集合{z|z=xy，x∈A，y∈B}中的元素的个数为 （　　）
    A．2B．3C．4D．5

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    3．已知集合A={x|x2-ax+a2-37=0}，B={x|x2-7x+12=0}，C={x|x2-2x-8=0}，求a为何值时，A∩B?∅与A∩C=∅同时成立？

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    13．已知${a}^{\frac{1}{2}}+{a}^{-\frac{1}{2}}$=3，求下列各式的值：
    （1）a+a-1．（2）a2+a-2；（3）a2-a-2．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    20．画出函数y=|log2x|与y=log$\frac{1}{2}$|x|的草图，并写出单调区间．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    17．已知函数f（x）=x2+2x+1．
    （1）g（x）为偶函数，且x≥0，g（x）=f（x），求g（x）的表达式；
    （2）求f（x）在区间[t，t+2]（t∈R）的最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    18．已知抛物线y=2x2+ax-1的顶点坐标为（1，b），则（　　）
    A．a＜4，b=3B．a=-4，b=3C．a=4，b=-3D．a=-4，b=-3

    查看答案和解析>>

    同步练习册答案