
【题目】已知函数f(x)=![]() x3
x3![]() (a2+a+2)x2+a2(a+2)x,a∈R.
(a2+a+2)x2+a2(a+2)x,a∈R.
(1)当a=![]() 1时,求函数y=f(x)的单调区间;
1时,求函数y=f(x)的单调区间;
(2)求函数y=f(x)的极值点.
【答案】(1)递增区间为(-∞,+∞);(2)见解析
【解析】
(1)先求解导数,利用导数取值的正负可得单调区间;
(2)先求解导数,结合导数零点情况判断函数极值点的情况.
(1)当a=![]() 1时,
1时,![]() .∵
.∵![]() =x2
=x2![]() 2x+1=(x
2x+1=(x![]() 1)2≥0,
1)2≥0,
故函数在R内为增函数,单调递增区间为(-∞,+∞).
(2)∵![]() =x2
=x2![]() (a2+a+2)x+a2(a+2)=(x
(a2+a+2)x+a2(a+2)=(x![]() a2)[x
a2)[x![]() (a+2)],
(a+2)],
①当a=![]() 1或a=2时,a2=a+2,∵
1或a=2时,a2=a+2,∵![]() ≥0恒成立,函数为增函数,无极值;
≥0恒成立,函数为增函数,无极值;
②当a<![]() 1或a>2时,a2>a+2,
1或a>2时,a2>a+2,
可得当x∈(![]() ∞,a+2)时,
∞,a+2)时,![]() >0,函数为增函数;
>0,函数为增函数;
当x∈(a+2,a2)时,![]() <0,函数为减函数;
<0,函数为减函数;
当x∈(a2,+∞)时,![]() >0,函数为增函数.
>0,函数为增函数.
当x=a+2时,函数有极大值f(a+2),当x=a2时,函数有极小值f(a2).
③当![]() 1<a<2时,a2<a+2.
1<a<2时,a2<a+2.
可得当x∈(-∞,a2)时,![]() >0,函数为增函数;
>0,函数为增函数;
当x∈(a2,a+2)时,![]() <0,函数为减函数;
<0,函数为减函数;
当x∈(a+2,+∞)时,![]() >0,函数为增函数.
>0,函数为增函数.
当x=a+2时,函数有极小值f(a+2);当x=a2时,函数有极大值f(a2).
综上可得:当a=![]() 1或a=2时,函数无极值点;当a<
1或a=2时,函数无极值点;当a<![]() 1或a>2时,函数有极大值点a+2,函数有极小值点a2;当
1或a>2时,函数有极大值点a+2,函数有极小值点a2;当![]() 1<a<2时,函数有极大值点a2,函数有极小值点a+2.
1<a<2时,函数有极大值点a2,函数有极小值点a+2.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】已知点![]() 在椭圆
在椭圆![]() 上,直线
上,直线![]() 与x,y轴分别交于A,B两点,0为坐标原点,且△OAB 的面积的最小值为
与x,y轴分别交于A,B两点,0为坐标原点,且△OAB 的面积的最小值为![]()

(1)求椭圆![]() 的离心率;
的离心率;
(2) 设点C、D、F2分别为椭圆![]() 的上、下顶点以及右焦点,E 为线段OD 的中点,直线F2E 与椭圆
的上、下顶点以及右焦点,E 为线段OD 的中点,直线F2E 与椭圆![]() 相交于M、N 两点,若
相交于M、N 两点,若![]() ,求椭圆
,求椭圆![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线Cn:x2﹣2nx+y2=0,(n=1,2,…).从点P(﹣1,0)向曲线Cn引斜率为kn(kn>0)的切线ln,切点为Pn(xn,yn).
(1)求数列{xn}与{yn}的通项公式;
(2)证明: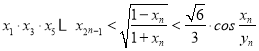 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】朱世杰是元代著名数学家,他所著《算学启蒙》是一部在中国乃至世界最早的科学普及著作.《算学启蒙》中提到一些堆垛问题,如“三角垛果子”,就是将一样大小的果子堆垛成正三棱锥,每层皆堆成正三角形,从上向下数,每层果子数分别为1,3,6,10,…,现有一个“三角垛果子”,其最底层每边果子数为10,则该层果子数为( )
A. 50B. 55C. 100D. 110
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的长轴长为4,左、右顶点分别为
的长轴长为4,左、右顶点分别为![]() ,经过点
,经过点![]() 的动直线与椭圆
的动直线与椭圆![]() 相交于不同的两点
相交于不同的两点![]() (不与点
(不与点![]() 重合).
重合).
(1)求椭圆![]() 的方程及离心率;
的方程及离心率;
(2)求四边形![]() 面积的最大值;
面积的最大值;
(3)若直线![]() 与直线
与直线![]() 相交于点
相交于点![]() ,判断点
,判断点![]() 是否位于一条定直线上?若是,写出该直线的方程. (结论不要求证明)
是否位于一条定直线上?若是,写出该直线的方程. (结论不要求证明)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 与x轴交于A,B两点,点Q的坐标为
与x轴交于A,B两点,点Q的坐标为![]() .
.
(1)是否存在b,使得![]() ,如果存在求出b值;如果不存在,说明理由;
,如果存在求出b值;如果不存在,说明理由;
(2)过A,B,Q三点的圆面积最小时,求圆的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的长轴长为6,离心率为
的长轴长为6,离心率为![]() .
.
(1)求椭圆C的标准方程;
(2)设椭圆C的左、右焦点分别为![]() ,
,![]() ,左、右顶点分别为A,B,点M,N为椭圆C上位于x轴上方的两点,且
,左、右顶点分别为A,B,点M,N为椭圆C上位于x轴上方的两点,且![]() ,记直线AM,BN的斜率分别为
,记直线AM,BN的斜率分别为![]() ,且
,且![]() ,求直线
,求直线![]() 的方程.
的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com