
【题目】如图,四棱锥![]() 中,
中,![]() 底面ABCD,
底面ABCD,![]() ,
,![]() ,
,![]() .
.
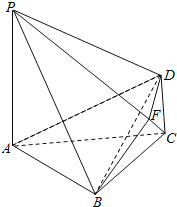
![]() Ⅰ
Ⅰ![]() 求证:
求证:![]() 平面PAC;
平面PAC;
![]() Ⅱ
Ⅱ![]() 若侧棱PC上的点F满足
若侧棱PC上的点F满足![]() ,求三棱锥
,求三棱锥![]() 的体积.
的体积.
【答案】(1)见解析 (2)![]()
【解析】
试题(1)由于![]() 可以证明
可以证明![]() 要证明
要证明![]() 只需证明
只需证明![]() 从而
从而![]() 中的两条相交直线,
中的两条相交直线,![]() (2)由(1)知
(2)由(1)知![]() 为等腰三角形,面积容易求出,考虑以BCD为底面.F为顶点 的三棱锥,以及以BCD为底面,P为顶点的三棱锥面积容易求出,所以
为等腰三角形,面积容易求出,考虑以BCD为底面.F为顶点 的三棱锥,以及以BCD为底面,P为顶点的三棱锥面积容易求出,所以![]()
试题解析:(1)证明:因为BC=CD,所以△BCD为等腰三角形,
又∠ACB=∠ACD,故BD⊥AC. 因为PA⊥底面ABCD,所以PA⊥BD.
从而BD与平面PAC内两条相交直线PA,AC都垂直, 所以BD⊥平面PAC.
(2)解:三棱锥PBCD的底面BCD的面积S△BCD=![]() BC·CD·sin∠BCD=
BC·CD·sin∠BCD=![]() ×2×2×sin
×2×2×sin![]() =
=![]() .
.
由PA⊥底面ABCD,得![]() =
=![]() ·S△BCD·PA=
·S△BCD·PA=![]() ×
×![]() ×2
×2![]() =2.
=2.
由PF=7FC,得三棱锥FBCD的高为![]() PA,
PA,
故![]() =
=![]() ·S△BCD·
·S△BCD·![]() PA=
PA=![]() ×
×![]() ×
×![]() ×2
×2![]() =
=![]() ,
,
所以![]() =
=![]() -
-![]() =2-
=2-![]() =
=![]() .
.


 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案科目:高中数学 来源: 题型:
【题目】已知![]() 为坐标原点,椭圆
为坐标原点,椭圆![]() :
:![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,
,![]() ,右顶点为
,右顶点为![]() ,上顶点为
,上顶点为![]() ,若
,若![]() ,
,![]() ,
,![]() 成等比数列,椭圆
成等比数列,椭圆![]() 上的点到焦点
上的点到焦点![]() 的距离的最大值为
的距离的最大值为![]() .
.
![]() 求椭圆
求椭圆![]() 的标准方程;
的标准方程;
![]() 过该椭圆的右焦点作两条互相垂直的弦
过该椭圆的右焦点作两条互相垂直的弦![]() 与
与![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() (a>b>0)的一个顶点为A(2,0),离心率为
(a>b>0)的一个顶点为A(2,0),离心率为![]() .直线y=k(x-1)与椭圆C交于不同的两点M,N.
.直线y=k(x-1)与椭圆C交于不同的两点M,N.
(1)求椭圆C的方程;
(2)当△AMN的面积为![]() 时,求k的值.
时,求k的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】黄冈市的天气预报显示,大别山区在今后的三天中,每一天有强浓雾的概率为![]() ,现用随机模拟的方法估计这三天中至少有两天有强浓雾的概率:先利用计算器产生
,现用随机模拟的方法估计这三天中至少有两天有强浓雾的概率:先利用计算器产生![]() 之间整数值的随机数,并用0,1,2,3,4,5表示没有强浓雾,用6,7,8,9表示有强浓雾,再以每3个随机数作为一组,代表三天的天气情况,产生了如下20组随机数:
之间整数值的随机数,并用0,1,2,3,4,5表示没有强浓雾,用6,7,8,9表示有强浓雾,再以每3个随机数作为一组,代表三天的天气情况,产生了如下20组随机数:
779 537 113 730 588 506 027 394 357 231
683 569 479 812 842 273 925 191 978 520
则这三天中至少有两天有强浓雾的概率近似为![]()
![]()
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,以
中,以![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,已知曲线
轴的正半轴为极轴建立极坐标系,已知曲线![]() 的极坐标方程为
的极坐标方程为![]() ,曲线
,曲线![]() 的极坐标方程为
的极坐标方程为![]() ,曲线
,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求![]() 与
与![]() 的直角坐标方程;
的直角坐标方程;
(2)若![]() 与
与![]() 的交于
的交于![]() 点,
点,![]() 与
与![]() 交于
交于![]() 、
、![]() 两点,求
两点,求![]() 的面积.
的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校参加高一年级期中考试的学生中随机抽出60名学生,将其数学成绩分成六段![]() 、
、![]() 、
、![]() 、
、![]() 后得到如图部分频率分布直方图,观察图形的信息,回答下列问题:
后得到如图部分频率分布直方图,观察图形的信息,回答下列问题:

![]() 求分数在
求分数在![]() 内的频率,并补全这个频率分布直方图;
内的频率,并补全这个频率分布直方图;
![]() 统计方法中,同一组数据常用该组区间的中点值作为代表,据此估计本次考试的平均分;
统计方法中,同一组数据常用该组区间的中点值作为代表,据此估计本次考试的平均分;
![]() 若从60名学生中随抽取2人,抽到的学生成绩在
若从60名学生中随抽取2人,抽到的学生成绩在![]() 记0分,在
记0分,在![]() 记1分,在
记1分,在![]() 记2分,用
记2分,用![]() 表示抽取结束后的总记分,求
表示抽取结束后的总记分,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在某公司举行的年终庆典活动中,主持人利用随机抽奖软件进行抽奖:由电脑随机生成一张如图所示的3![]() 3表格,其中1格设奖300元,4格各设奖200元,其余4格各设奖100元,点击某一格即显示相应金额.某人在一张表中随机不重复地点击3格,记中奖的总金额为X元.
3表格,其中1格设奖300元,4格各设奖200元,其余4格各设奖100元,点击某一格即显示相应金额.某人在一张表中随机不重复地点击3格,记中奖的总金额为X元.
(1)求概率![]() ;
;
(2)求![]() 的概率分布及数学期望
的概率分布及数学期望![]() .
.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】椭圆C:![]() 的离心率为
的离心率为![]() ,其右焦点到椭圆C外一点
,其右焦点到椭圆C外一点![]() 的距离为
的距离为![]() ,不过原点O的直线l与椭圆C相交于A,B两点,且线段AB的长度为2.
,不过原点O的直线l与椭圆C相交于A,B两点,且线段AB的长度为2.
![]() 1
1![]() 求椭圆C的方程;
求椭圆C的方程;
![]() 2
2![]() 求
求![]() 面积S的最大值.
面积S的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com