
【题目】函数![]() 有3个不同零点,则实数a的取值范围____
有3个不同零点,则实数a的取值范围____
【答案】![]()
【解析】
先求出当x<0时,函数f(x)有一个零点,然后得到当x≥﹣1时,有两个不同的零点,然后转化为两个函数的图象的交点个数问题,利用数形结合进行求解即可.
解:当x<﹣1时,由f(x)=0得x2﹣2ax=0,得a![]() ,
,
∵x<﹣1,∴a![]() 且此时函数f(x)只有一个零点,
且此时函数f(x)只有一个零点,
要使f(x)有3个不同零点,则等价为当x≥﹣1时,f(x)=0有且只有2个不同的零点,
由f(x)=ex﹣|x﹣a|=0得ex=|x﹣a|,
作出函数g(x)=ex和h(x)=|x﹣a|在x≥﹣1的图象如图,

当x≥a时,h(x)=x﹣a,当h(x)与g(x)相切时,g′(x)=ex,由g′(x)=ex=1得x=0,此时g(0)=1,即切点坐标为A(0,1),
此时h(0)=0﹣a=1,得a=﹣1,
当x=﹣1时,g(﹣1)![]() ,当直线h(x)=x﹣a经过点B(﹣1,
,当直线h(x)=x﹣a经过点B(﹣1,![]() )时,﹣1﹣a
)时,﹣1﹣a![]() ,
,
则a=﹣1![]() ,
,
要使ex=|x﹣a|在x≥﹣1时,有两个不同的交点,
则直线h(x)=x﹣a应该在过A和B的直线之间,
则﹣1![]() a<﹣1,
a<﹣1,
即实数a的取值范围是[﹣1![]() ,﹣1),
,﹣1),
故答案为:[﹣1![]() ,﹣1)
,﹣1)


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】若无穷数列![]() 满足:
满足:![]() ,且对任意正整数
,且对任意正整数![]() ,
,![]() 都为
都为![]() 中等于
中等于![]() 的项的个数,则称数列
的项的个数,则称数列![]() 为“
为“![]() 数列”.
数列”.
(1)请列举出三个![]() 数列,每个
数列,每个![]() 数列只写出其前5项;
数列只写出其前5项;
(2)若数列![]() 为一个
为一个![]() 数列,证明:
数列,证明:![]() ,都有
,都有![]() ;
;
(3)若数列![]() 为一个
为一个![]() 数列,求集合
数列,求集合![]() 中元素个数的最大值.
中元素个数的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
以直角坐标系的原点![]() 为极点,
为极点, ![]() 轴的正半轴为极轴建立极坐标系,已知点
轴的正半轴为极轴建立极坐标系,已知点![]() 的直角坐标为
的直角坐标为![]() ,若直线
,若直线![]() 的极坐标方程为
的极坐标方程为![]() 曲线
曲线![]() 的参数方程是
的参数方程是![]() (
(![]() 为参数).
为参数).
(1)求直线![]() 和曲线
和曲线![]() 的普通方程;
的普通方程;
(2)设直线![]() 和曲线
和曲线![]() 交于
交于![]() 两点,求
两点,求![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆E:![]() 的焦点在
的焦点在![]() 轴上,A是E的左顶点,斜率为k (k > 0)的直线交E于A,M两点,点N在E上,MA⊥NA.
轴上,A是E的左顶点,斜率为k (k > 0)的直线交E于A,M两点,点N在E上,MA⊥NA.
(Ⅰ)当t=4,![]() 时,求△AMN的面积;
时,求△AMN的面积;
(Ⅱ)当![]() 时,求k的取值范围.
时,求k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,某公园内有一块矩形绿地区域ABCD,已知AB=100米,BC=80米,以AD,BC为直径的两个半圆内种植花草,其它区域种值苗木. 现决定在绿地区域内修建由直路BN,MN和弧形路MD三部分组成的观赏道路,其中直路MN与绿地区域边界AB平行,直路为水泥路面,其工程造价为每米2a元,弧形路为鹅卵石路面,其工程造价为每米3a元,修建的总造价为W元. 设![]() .
.
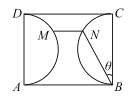
(1)求W关于![]() 的函数关系式;
的函数关系式;
(2)如何修建道路,可使修建的总造价最少?并求最少总造价.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了政府对过热的房地产市场进行调控决策,统计部门对城市人和农村人进行了买房的心理预期调研,用简单随机抽样的方法抽取110人进行统计,得到如下列联表:
买房 | 不买房 | 纠结 | |
城市人 | 5 | 15 | |
农村人 | 20 | 10 |
已知样本中城市人数与农村人数之比是3:8.
![]() 分别求样本中城市人中的不买房人数和农村人中的纠结人数;
分别求样本中城市人中的不买房人数和农村人中的纠结人数;
![]() 用独立性检验的思想方法说明在这三种买房的心理预期中哪一种与城乡有关?
用独立性检验的思想方法说明在这三种买房的心理预期中哪一种与城乡有关?
参考公式:![]() .
.
|
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com