
【题目】已知函数![]() ,曲线
,曲线![]() 在点
在点![]() 处的切线方程为
处的切线方程为![]()
(1) 求![]() 的值;
的值;
(2) 证明: ![]() .
.
【答案】(1)![]() ;(2)见解析
;(2)见解析
【解析】分析:第一问结合导数的几何意义以及切点在切线上也在函数图像上,从而建立关于![]() 的等量关系式,从而求得结果;第二问可以有两种方法,一是将不等式转化,构造新函数,利用导数研究函数的最值,从而求得结果,二是利用中间量来完成,这样利用不等式的传递性来完成,再者这种方法可以简化运算.
的等量关系式,从而求得结果;第二问可以有两种方法,一是将不等式转化,构造新函数,利用导数研究函数的最值,从而求得结果,二是利用中间量来完成,这样利用不等式的传递性来完成,再者这种方法可以简化运算.
详解:(1)解:![]() ,由题意有
,由题意有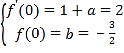 ,解得
,解得![]()
(2)证明:(方法一)由(1)知,![]() .设
.设![]()
则只需证明![]()
![]()
![]() ,设
,设![]()
则![]() ,
, ![]() 在
在![]() 上单调递增
上单调递增
![]() ,
,![]()
![]() ,使得
,使得![]()
且当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]()
![]() 当
当![]() 时,
时,![]() ,
,![]() 单调递减
单调递减
当![]() 时,
时,![]() ,
,![]() 单调递增
单调递增
![]()
![]() ,由
,由![]() ,得
,得![]() ,
,
![]()
![]()
![]() ,
,
设![]() ,
,![]() ,
,![]()
![]()
![]() 当
当![]() 时,
时,![]() ,
,![]() 在
在![]() 单调递减,
单调递减,
![]()
![]()
![]()
![]()
![]() ,因此
,因此![]()
(方法二)先证当![]() 时,
时,![]()
![]() ,即证
,即证![]()
设![]() ,
,![]() 则
则![]() ,且
,且![]()
![]() ,
,![]() 在
在![]() 单调递增,
单调递增,![]()
![]() 在
在![]() 单调递增,则当
单调递增,则当![]() 时,
时,![]()
(也可直接分析![]()
![]()
![]()
![]()
![]() 显然成立)
显然成立)
再证![]()
设![]() ,则
,则![]() ,令
,令![]() ,得
,得![]()
且当![]() 时,
时,![]() ,
,![]() 单调递减;
单调递减;
当![]() 时,
时,![]() ,
,![]() 单调递增.
单调递增.
![]()
![]()
![]() ,即
,即![]()
又![]() ,
,![]()


 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() (a>b>0)的一个顶点为A(2,0),离心率为
(a>b>0)的一个顶点为A(2,0),离心率为![]() .直线y=k(x-1)与椭圆C交于不同的两点M,N.
.直线y=k(x-1)与椭圆C交于不同的两点M,N.
(1)求椭圆C的方程;
(2)当△AMN的面积为![]() 时,求k的值.
时,求k的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在某公司举行的年终庆典活动中,主持人利用随机抽奖软件进行抽奖:由电脑随机生成一张如图所示的3![]() 3表格,其中1格设奖300元,4格各设奖200元,其余4格各设奖100元,点击某一格即显示相应金额.某人在一张表中随机不重复地点击3格,记中奖的总金额为X元.
3表格,其中1格设奖300元,4格各设奖200元,其余4格各设奖100元,点击某一格即显示相应金额.某人在一张表中随机不重复地点击3格,记中奖的总金额为X元.
(1)求概率![]() ;
;
(2)求![]() 的概率分布及数学期望
的概率分布及数学期望![]() .
.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】椭圆C:![]() 的离心率为
的离心率为![]() ,其右焦点到椭圆C外一点
,其右焦点到椭圆C外一点![]() 的距离为
的距离为![]() ,不过原点O的直线l与椭圆C相交于A,B两点,且线段AB的长度为2.
,不过原点O的直线l与椭圆C相交于A,B两点,且线段AB的长度为2.
![]() 1
1![]() 求椭圆C的方程;
求椭圆C的方程;
![]() 2
2![]() 求
求![]() 面积S的最大值.
面积S的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com