
【题目】黄冈市的天气预报显示,大别山区在今后的三天中,每一天有强浓雾的概率为![]() ,现用随机模拟的方法估计这三天中至少有两天有强浓雾的概率:先利用计算器产生
,现用随机模拟的方法估计这三天中至少有两天有强浓雾的概率:先利用计算器产生![]() 之间整数值的随机数,并用0,1,2,3,4,5表示没有强浓雾,用6,7,8,9表示有强浓雾,再以每3个随机数作为一组,代表三天的天气情况,产生了如下20组随机数:
之间整数值的随机数,并用0,1,2,3,4,5表示没有强浓雾,用6,7,8,9表示有强浓雾,再以每3个随机数作为一组,代表三天的天气情况,产生了如下20组随机数:
779 537 113 730 588 506 027 394 357 231
683 569 479 812 842 273 925 191 978 520
则这三天中至少有两天有强浓雾的概率近似为![]()
![]()
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
科目:高中数学 来源: 题型:
【题目】如图,正六边形![]() 的中心为
的中心为![]() ,对
,对![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 这七个点中的任意两点,以其中一点为起点、另一点为终点作向量.任取其中两个向量,以它们的数量积的绝对值作为随机变量
这七个点中的任意两点,以其中一点为起点、另一点为终点作向量.任取其中两个向量,以它们的数量积的绝对值作为随机变量![]() .试求
.试求![]() 的概率分布列及其数学期望
的概率分布列及其数学期望![]() .
.

查看答案和解析>>
科目:高中数学 来源: 题型:
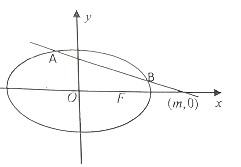
【题目】已知椭圆![]() 的右焦点F与抛物线
的右焦点F与抛物线![]() 焦点重合,且椭圆的离心率为
焦点重合,且椭圆的离心率为![]() ,过
,过![]() 轴正半轴一点
轴正半轴一点![]() 且斜率为
且斜率为![]() 的直线
的直线![]() 交椭圆于
交椭圆于![]() 两点.
两点.
(1)求椭圆的标准方程;
(2)是否存在实数![]() 使以线段
使以线段![]() 为直径的圆经过点
为直径的圆经过点![]() ,若存在,求出实数
,若存在,求出实数![]() 的值;若不存在说明理由.
的值;若不存在说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
以直角坐标系的原点![]() 为极点,
为极点, ![]() 轴的正半轴为极轴建立极坐标系,已知点
轴的正半轴为极轴建立极坐标系,已知点![]() 的直角坐标为
的直角坐标为![]() ,若直线
,若直线![]() 的极坐标方程为
的极坐标方程为![]() 曲线
曲线![]() 的参数方程是
的参数方程是![]() (
(![]() 为参数).
为参数).
(1)求直线![]() 和曲线
和曲线![]() 的普通方程;
的普通方程;
(2)设直线![]() 和曲线
和曲线![]() 交于
交于![]() 两点,求
两点,求![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某媒体为调查喜爱娱乐节目![]() 是否与观众性别有关,随机抽取了30名男性和30名女性观众,抽查结果用等高条形图表示如图:
是否与观众性别有关,随机抽取了30名男性和30名女性观众,抽查结果用等高条形图表示如图:
喜欢节目A | 不喜欢节目A | 总计 | |
男性观众 | |||
女性观众 | |||
总计 |
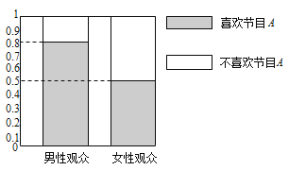
(1)根据该等高条形图,完成右上![]() 列联表,并用独立性检验的方法分析,则在犯错误的概率不超过多少的前提下认为喜欢娱乐节目
列联表,并用独立性检验的方法分析,则在犯错误的概率不超过多少的前提下认为喜欢娱乐节目![]() 与观众性别有关?
与观众性别有关?
(2)从男性观众中按喜欢节目![]() 与否,用分层抽样的方法抽取5名做进一步调查.从这5名中任选2名,求恰有1名喜欢节目
与否,用分层抽样的方法抽取5名做进一步调查.从这5名中任选2名,求恰有1名喜欢节目![]() 和1名不喜欢节目
和1名不喜欢节目![]() 的概率.
的概率.
附: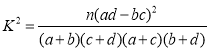
| 0.100 | 0.050 | 0.010 | 0.00 |
| 2.706 | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,某公园内有一块矩形绿地区域ABCD,已知AB=100米,BC=80米,以AD,BC为直径的两个半圆内种植花草,其它区域种值苗木. 现决定在绿地区域内修建由直路BN,MN和弧形路MD三部分组成的观赏道路,其中直路MN与绿地区域边界AB平行,直路为水泥路面,其工程造价为每米2a元,弧形路为鹅卵石路面,其工程造价为每米3a元,修建的总造价为W元. 设![]() .
.
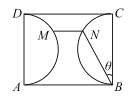
(1)求W关于![]() 的函数关系式;
的函数关系式;
(2)如何修建道路,可使修建的总造价最少?并求最少总造价.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com