
设函数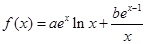 ,曲线
,曲线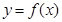 在点
在点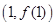 处的切线为
处的切线为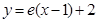 .
.
(1)求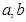 ;
;
(2)证明: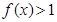 .
.
(1) 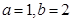 ;(2)详见解析.
;(2)详见解析.
解析试题分析:(1)求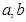 的值就一定要建立关于
的值就一定要建立关于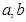 的两个方程,通过解方程求出
的两个方程,通过解方程求出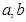 值,这就是方程思想,这里通过斜率关系确立一个方程,还有一个方程就是要用切点
值,这就是方程思想,这里通过斜率关系确立一个方程,还有一个方程就是要用切点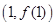 既在直线上,又在曲线上来确立,即用好切点的双重身份;(2)通过重新构造函数,利用导数知识来研究函数的极值和最值,进而达到证明不等式的目的,此题如果想直接去研究
既在直线上,又在曲线上来确立,即用好切点的双重身份;(2)通过重新构造函数,利用导数知识来研究函数的极值和最值,进而达到证明不等式的目的,此题如果想直接去研究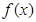 的最小值,通过最小值比
的最小值,通过最小值比 大,来达到证题的目的,那是很难办到的,所以说构造函数是需要功底的,也是需要技巧的.
大,来达到证题的目的,那是很难办到的,所以说构造函数是需要功底的,也是需要技巧的.
试题解析:(1) 函数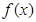 的定义域为
的定义域为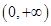 ,
,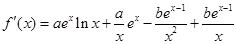 ,根据切点
,根据切点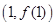 既在直线上,又在曲线上,依题意可得
既在直线上,又在曲线上,依题意可得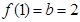 ,
,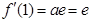 ,故
,故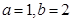 4分
4分
(2)由(1)知,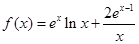 ,从而
,从而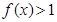 等价于
等价于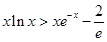 .
.
设函数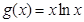 ,则
,则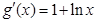 ,所以当
,所以当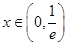 时,
时,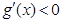 ,当
,当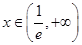 时,
时,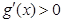 ,故
,故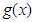 在
在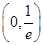 单调递减,在
单调递减,在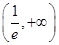 单调递增,从而
单调递增,从而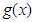 在
在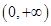 上的最小值为
上的最小值为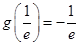 10分
10分
设函数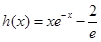 ,则
,则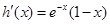 ,所以当
,所以当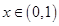 时,
时,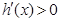 ,当
,当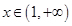 时,
时, ,故
,故 在
在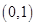 单调递增,在
单调递增,在 单调递减,从而
单调递减,从而 在
在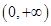 上的最大值为
上的最大值为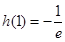 .又
.又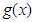 和
和 在
在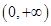 上取得最值的条件不同,所以综上:当
上取得最值的条件不同,所以综上:当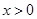 时,
时,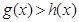 ,即
,即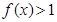 . 14分
. 14分
考点:1.导数及其应用;2.函数的综合应用.


湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com