
设各项均为正数的数列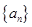 的前
的前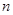 项和为
项和为 ,且
,且 满足
满足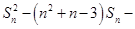
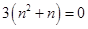 ,
, .
.
(1)求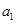 的值;
的值;
(2)求数列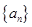 的通项公式;
的通项公式;
(3)证明:对一切正整数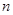 ,有
,有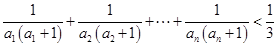 .
.
(1)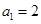 ;(2)
;(2)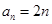 ;(3)详见解析.
;(3)详见解析.
解析试题分析:(1)将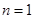 代入方程
代入方程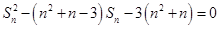 得到
得到 ,结合题中条件(数列
,结合题中条件(数列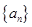 的各项均为正数,得到
的各项均为正数,得到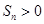 )求出
)求出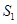 的值,从而得到
的值,从而得到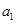 的值;(2)由十字相乘法结合
的值;(2)由十字相乘法结合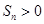 得到
得到 的表达式,然后在
的表达式,然后在 的情况下,由
的情况下,由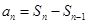 求出数列
求出数列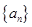 的表达式,并验证
的表达式,并验证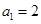 是否满足该表达式,从而得到数列
是否满足该表达式,从而得到数列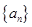 的通项公式;(3)解法一是利用放缩法得到
的通项公式;(3)解法一是利用放缩法得到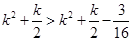
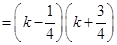 ,于是得到
,于是得到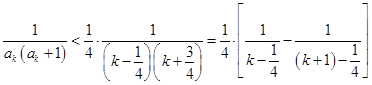 ,最后利用裂项求和法证明题中的不等式;解法二是保持
,最后利用裂项求和法证明题中的不等式;解法二是保持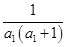 不放缩,在
不放缩,在 的条件下放缩为
的条件下放缩为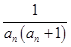
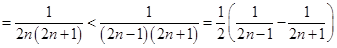 ,最后在
,最后在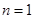 和
和 时利用放缩法结合裂项法证明相应的不等式.
时利用放缩法结合裂项法证明相应的不等式.
(1)令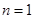 得:
得: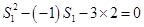 ,即
,即 ,
,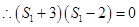 ,
, ,
,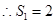 ,即
,即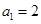 ;
;
(2)由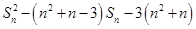 ,得
,得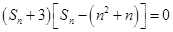 ,
,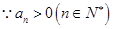 ,
,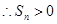 ,从而
,从而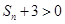 ,
,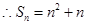 ,
,
所以当 时,
时,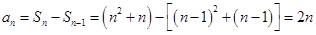 ,
,
又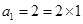 ,
,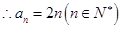 ;
;
(3)解法一:当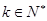 时,
时, ,
,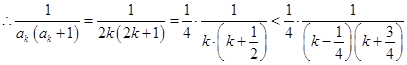
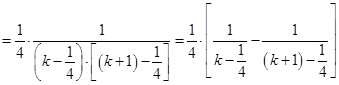
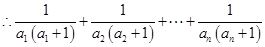
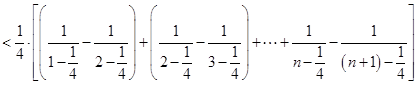
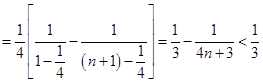 .
.
证法二:当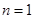 时,
时,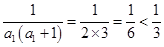 成立,
成立,
当 时,
时,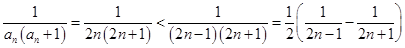 ,
,
则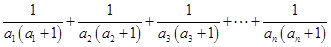
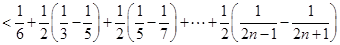
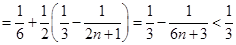 .
.
考点:本题以二次方程的形式以及 与
与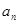 的关系考查数列通项的求解,以及利用放缩法证明数列不等式的综合问题,考查学生的计算能力与逻辑推理能力,属于中等偏难题.
的关系考查数列通项的求解,以及利用放缩法证明数列不等式的综合问题,考查学生的计算能力与逻辑推理能力,属于中等偏难题.


科目:高中数学 来源: 题型:解答题
设数列 的前
的前 项和为
项和为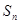 ,对任意的正整数
,对任意的正整数 ,都有
,都有 成立,记
成立,记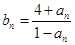 .(1)(1)求数列
.(1)(1)求数列 与数列
与数列 的通项公式;
的通项公式;
(2)设数列 的前
的前 项和为
项和为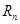 ,是否存在正整数
,是否存在正整数 ,使得
,使得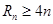 成立?若存在,找出一个正整数
成立?若存在,找出一个正整数 ;若不存在,请说明理由.
;若不存在,请说明理由.
(3)记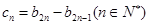 ,设数列
,设数列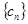 的前
的前 项和为
项和为 ,求证:对于
,求证:对于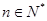 都有
都有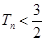
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
水土流失是我国西部大开发中最突出的问题,全国9100万亩坡度为25°以上的坡耕地需退耕还林,其中西部占70%,2002年国家确定在西部地区退耕还林面积为515万亩,以后每年退耕土地面积递增12%.
(1)试问,从2002年起到哪一年西部地区基本上解决退耕还林问题?
(2)为支持退耕还林工作,国家财政补助农民每亩300斤粮食,每斤粮食按0.7元计算,并且每亩退耕地每年补助20元,试问到西部地区基本解决退耕还林问题时,国家财政共需支付约多少亿元?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知数列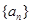 的奇数项是首项为1的等差数列,偶数项是首项为2的等比数列.数列
的奇数项是首项为1的等差数列,偶数项是首项为2的等比数列.数列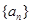 前
前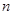 项和为
项和为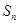 ,且满足
,且满足
(1)求数列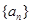 的通项公式;
的通项公式;
(2)求数列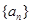 前
前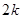 项和
项和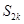 ;
;
(3)在数列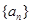 中,是否存在连续的三项
中,是否存在连续的三项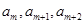 ,按原来的顺序成等差数列?若存在,求出所有满足条件的正整数
,按原来的顺序成等差数列?若存在,求出所有满足条件的正整数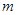 的值;若不存在,说明理由.
的值;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com