
在一个特定时段内,以点E为中心的7n mile以内海域被设为警戒水域.点E正北55n mile处有一个雷达观测站A,某时刻测得一艘匀速直线行驶的船只位于点A北偏东45°且与点A相距40 n mile的位置B,经过40分钟又测得该船已行驶到点A北偏东
n mile的位置B,经过40分钟又测得该船已行驶到点A北偏东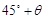 (其中
(其中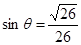 ,
,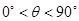 )且与点A相距10
)且与点A相距10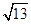 n mile的位置C.
n mile的位置C.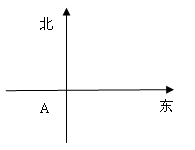
(I)求该船的行驶速度(单位:n mile /h);
(II)若该船不改变航行方向继续行驶.判断它是否会进入警戒水域,并说明理由.
(I)船的行驶速度为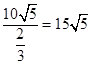 (海里/小时).(II)船会进入警戒水域.
(海里/小时).(II)船会进入警戒水域.
解析试题分析:(I)根据同角三角函数的基本关系式求出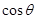 ,然后利用余弦定理求出BC的值,从而可求出船的行驶速度.
,然后利用余弦定理求出BC的值,从而可求出船的行驶速度.
(II)判断船是否会进入警戒水域,关键是看点E到直线l的距离与半径7的关系,因而可求出直线l的方程,以及E点坐标,然后再根据点到直线的距离公式得到结论.
(I)如图,AB=40 ,AC=10
,AC=10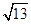 ,
,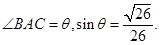
由于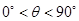 ,所以cos
,所以cos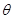 =
=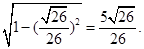
由余弦定理得BC=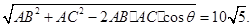
所以船的行驶速度为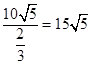 (海里/小时).
(海里/小时).
(II)解法一 如图所示,以A为原点建立平面直角坐标系,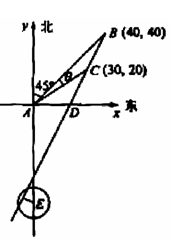
设点B、C的坐标分别是B(x1,y2), C(x1,y2),
BC与x轴的交点为D.
由题设有,x1=y1= 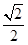 AB=40,
AB=40,
x2=ACcos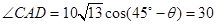 ,
,
y2=ACsin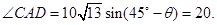
所以过点B、C的直线l的斜率k=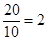 ,直线l的方程为y=2x-40.
,直线l的方程为y=2x-40.
又点E(0,-55)到直线l的距离d=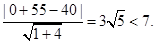
所以船会进入警戒水域.
解法二: 如图所示,设直线AE与BC的延长线相交于点Q.
在△ABC中,由余弦定理得,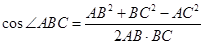 =
=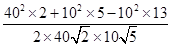 =
=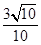 .
.
从而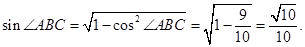
在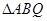 中,由正弦定理得,AQ=
中,由正弦定理得,AQ=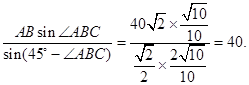
由于AE=55>40=AQ,所以点Q位于点A和点E之间,且QE=AE-AQ=15.
过点E作EP 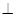 BC于点P,则EP为点E到直线BC的距离.
BC于点P,则EP为点E到直线BC的距离.
在Rt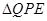 中,PE=QE·sin
中,PE=QE·sin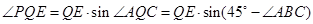
=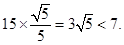 所以船会进入警戒水域.
所以船会进入警戒水域.
考点:正余弦定理在解三角形当中的应用,直线方程,点到直线的距离,直线与圆的位置关系.
点评:掌握正余弦定理及能解决的三角形类型是解三角形的前提.第(II)问关键是知道如何判断船是否会进入警戒水域,实质是直线与圆的位置关系的判断.


科目:高中数学 来源: 题型:解答题
(本小题满分12分)
已知在锐角△ABC中,a, b, c分别为角A、B、C所对的边,向量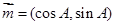 ,
,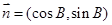 ,
,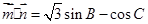 .
.
(1)求角A的大小;
(2)若a=3,求△ABC面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)
在△ABC中,内角A、B、C所对边的长分别为a、b、c,已知向量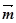 ="(1,cosA" -1),
="(1,cosA" -1),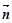 =(cosA,1)且满足
=(cosA,1)且满足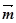 ⊥
⊥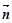 .
.
(Ⅰ)求A的大小;
(Ⅱ)若a= ,b+c=3 求b、c的值.
,b+c=3 求b、c的值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
在某海滨城市附近海面有一台风,据检测,当前台风中心位于城市O(如图)的东偏南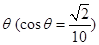 方向300 km的海面P处,并以20 km / h的速度向西偏北
方向300 km的海面P处,并以20 km / h的速度向西偏北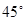 的方向移动,台风侵袭的范围为圆形区域,当前半径为60 km ,并以10 km / h的速度不断增加,问几小时后该城市开始受到台风的侵袭?持续多长时间?
的方向移动,台风侵袭的范围为圆形区域,当前半径为60 km ,并以10 km / h的速度不断增加,问几小时后该城市开始受到台风的侵袭?持续多长时间?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com