

分析 (Ⅰ)求出样本容量,从而求出a的值,和平均数;
(Ⅱ)厨霸有0.0150×10×40=6人,分别记为a1,a2,a3,a4,a5,a6,厨神有0.0075×10×40=3人,分别记为b1,b2,b3,共9人列出事件A包含的基本事件,从而求出满足条件的概率即可.
解答 解:(Ⅰ)由题意可知,样本容量$n=\frac{5}{0.0125×10}=40$,
所以$a=\frac{3}{40×10}=0.0075$.
所以平均成绩为55×0.125+65×0.2+75×0.45+85×0.15+95×0.075=73.5.
(Ⅱ)由题意可知,厨霸有0.0150×10×40=6人,分别记为a1,a2,a3,a4,a5,a6,厨神有0.0075×10×40=3人,分别记为b1,b2,b3,共9人.
从中任意抽取2人共有36种情况:(a1,a2),(a1,a3),(a1,a4),(a1,a5),(a1,a6),(a1,b1),(a1,b2),(a1,b3),(a2,a3),(a2,a4),(a2,a5),(a2,a6),(a2,b1),(a2,b2),(a2,b3),(a3,a4),(a3,a5),(a3,a6),(a3,b1),(a3,b2),(a3,b3),(a4,a5),(a4,a6),(a4,b1),(a4,b2),(a4,b3),(a5,a6),(a5,b1),(a5,b2),(a5,b3),(a6,b1),(a6,b2),(a6,b3),(b1,b2),(b1,b3),(b2,b3),
其中至少有1人是厨神的情况有21种,
所以至少有1人是厨神的概率为$\frac{21}{36}$=$\frac{7}{12}$.
点评 本题考查了频率分布直方图,茎叶图,考查满足条件的基本事件的概率问题,是一道中档题.


科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | $\sqrt{5}$ | C. | $\sqrt{6}$ | D. | $\sqrt{7}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {-1,1} | B. | {1} | C. | {0} | D. | {-1,0} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
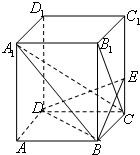 如图,已知正四棱柱ABCD-A1B1C1D1中,2AB=BB1,过点B作B1C的垂线交侧棱CC1于点E.
如图,已知正四棱柱ABCD-A1B1C1D1中,2AB=BB1,过点B作B1C的垂线交侧棱CC1于点E.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x=$\frac{kπ}{2}$-$\frac{π}{6}$ (k∈Z) | B. | x=$\frac{kπ}{2}$+$\frac{π}{6}$ (k∈Z) | C. | x=$\frac{kπ}{2}$-$\frac{π}{12}$ (k∈Z) | D. | x=$\frac{kπ}{2}$+$\frac{π}{12}$ (k∈Z) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com