
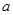 表示.
表示.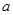 的值;
的值;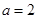 时,分别从甲,乙两组同学中各随机选取一名同学,求这两名同学的数学成绩之差的绝对值不超过2分的概率.
时,分别从甲,乙两组同学中各随机选取一名同学,求这两名同学的数学成绩之差的绝对值不超过2分的概率.
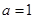 ;(2)
;(2)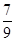 .
.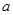 的值;
的值;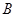 ,当
,当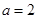 时,分别从甲、乙两组同学中各随机选取一名同学,所有可能的成绩结果有
时,分别从甲、乙两组同学中各随机选取一名同学,所有可能的成绩结果有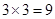 种,用枚举法列出所有可能的成绩结果,易得事件
种,用枚举法列出所有可能的成绩结果,易得事件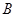 的结果有7种,因此这两名同学的数学成绩之差的绝对值不超过2分的概率
的结果有7种,因此这两名同学的数学成绩之差的绝对值不超过2分的概率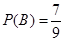 .
.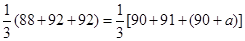 , 解得
, 解得 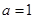 .
. 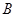 ,
,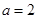 时,分别从甲、乙两组同学中各随机选取一名同学,所有可能的成绩结果有
时,分别从甲、乙两组同学中各随机选取一名同学,所有可能的成绩结果有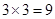 种, 它们是:
种, 它们是: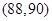 ,
,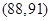 ,
,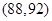 ,
,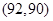 ,
,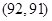 ,
,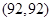 ,
,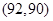 ,
,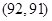 ,
,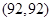 ,
,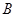 的结果有7种,它们是:
的结果有7种,它们是: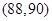 ,
,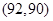 ,
,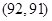 ,
,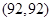 ,
,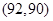 ,
,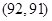 ,
,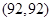 .
.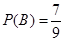 .
. 

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源:不详 题型:单选题
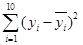 的值为( )
的值为( )| A.241.1 | B.245.1 | C.2411 | D.2451 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
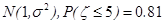 ,则
,则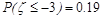 ;
;| A.4 | B.3 | C.2 | D.1 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| | 嗜酒 | 不嗜酒 | 总计 |
| 患肝病 | 7 775 | 42 | 7 817 |
| 未患肝病 | 2 099 | 49 | 2 148 |
| 总计 | 9 874 | 91 | 9 965 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 的频数分布表如下:
的频数分布表如下:| 分数 |  | 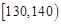 | 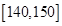 |
| 频数 | 60 | 20 | 20 |
 ,
, 和
和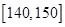 的同学中共抽取
的同学中共抽取 人,其中成绩在
人,其中成绩在 的有几人?
的有几人? 人中,任取
人中,任取 人,求成绩在
人,求成绩在 和
和 中各有
中各有 人的概率?
人的概率?查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| | 男 | 女 | 总计 |
| 爱好 | 40 | 20 | 60 |
| 不爱好 | 20 | 30 | 50 |
| 总计 | 60 | 50 | 110 |
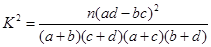 算得
算得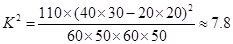
 | 0.050 | 0.010 | 0.001 |
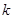 | 3.841 | 6.635 | 10.828 |
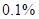 的前提下,认为“爱好该项运动与性别有关”
的前提下,认为“爱好该项运动与性别有关”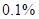 的前提下,认为“爱好该项运动与性别无关”
的前提下,认为“爱好该项运动与性别无关”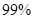 以上的把握认为“爱好该项运动与性别有关”
以上的把握认为“爱好该项运动与性别有关”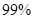 以上的把握认为“爱好该项运动与性别有关”
以上的把握认为“爱好该项运动与性别有关” 查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
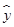 =0.30x+9.99.根据建设项目的需要,28天后混凝土的抗压度不得低于89.7 kg/cm2,每立方米混凝土的水泥用量最少应为________kg.(精确到0.1 kg)
=0.30x+9.99.根据建设项目的需要,28天后混凝土的抗压度不得低于89.7 kg/cm2,每立方米混凝土的水泥用量最少应为________kg.(精确到0.1 kg)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com