Question

关于x的不等式ax²+bx+c＞0的解集为{x|m＜x＜n，m＞0}
（1）试判断a，b，c的符号；
（2）求关于x的不等式cx²-bx+a＞0的解集．

Answer 1

解：（1）∵关于x的不等式ax²+bx+c＞0的解集为{x|m＜x＜n，m＞0}
∴m+n=-＞0，m•n=＞0，且a＜0，
∴c＜0，b＞0；
（2）不等式cx²-bx+a＞0等价于
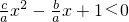
∴mn•x²+（m+n）x+1＜0
∴（mx+1）（nx+1）＜0
∵0＜m＜n
∴
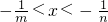
∴不等式的解集为．
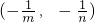
分析：（1）利用关于x的不等式ax²+bx+c＞0的解集为{x|m＜x＜n，m＞0}，结合韦达定理，即可判断a，b，c的符号；
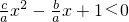
（2）不等式cx²-bx+a＞0等价于，利用（1）的结论，即可求解．
点评：本题考查解不等式，考查韦达定理的运用，考查学生的计算能力，属于基础题．