Question

8．已知函数f（x）=$\frac{1}{3}$ax³+$\frac{1}{2}$bx²+x，g（x）=$\frac{1}{3}$a²x³+$\frac{1}{2}$bx²+x，其中a＞0，若函数g（x）存在两个极值点x₁，x₂，且点x₁＜x₂．
（1）求证：函数f（x）的导函数f′（x）在（-1，1）上是单调函数；
（2）当a＞1时，函数f（x）也存在两个极值点x₃，x₄，且x₃＜x₄，是判断x₁，x₂，x₃，x₄的大小关系．

Answer 1

分析 （1）g′（x）=0有两个不等的实根，得它的根的判别式△=b²-4a²＞0，再两次求导f″（x），得f″（-1）f″（1）＞0，说明一次函数f″（x）=2ax+b在区间（-1，1）的符号均为正数，或均为负数，得出结论；
（2）构造两个函数：F（x）=f′（x）-1，G（x）=g′（x）-1，通过讨论它们的零点，得出它们的根之间的大小关系．然后通过分类讨论和在同一坐标系里作出F（x）和G（x）的图象，然后将两个图象向上平移一个单位，可得x₁，x₂，x₃，x₄的大小关系，最后综合可得出正确的大小关系．

解答 解：（1）∵g（x）=$\frac{1}{3}$a²x³+$\frac{1}{2}$bx²+x，
∴g′（x）=a²x²+bx+1，
∵函数g（x）存在两个极值点x₁，x₂，且点x₁＜x₂，a＞0，
∴g′（x）=0有两个不等的实根，
∴△=b²-4a²＞0，
∵f（x）=$\frac{1}{3}$ax³+$\frac{1}{2}$bx²+x，
∴f′（x）=ax²+bx+1，
∴f″（x）=2ax+b，
∴f″（1）f″（-1）=（b+2a）（b-2a）=b²-4a²＞0，
∴导函数f′（x）在（-1，1）上是单调函数；
（2）记函数F（x）=f′（x）-1=ax²+bx，G（x）=g′（x）-1=a²x²+bx
两个函数有公共的零点x=0，此外F（x）还有一个零点x=-$\frac{b}{a}$，G（x）还有一个零点x=-$\frac{b}{{a}^{2}}$，
①因为a＞1，当b＜0时由（1）得必定有0＜-$\frac{b}{{a}^{2}}$＜-$\frac{b}{a}$，
在同一坐标系里作出F（x）和G（x）的图象：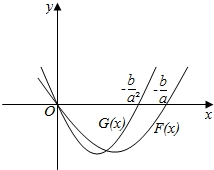

将此两个图象都上移一个单位，可得函数f′（x）和g′（x）的图象
所以由图象可得x₁＜x₃＜x₂＜x₄
②当b＞0时，同理可得四个根的大小关系：x₁＜x₃＜x₂＜x₄
综上所述，可判断x₁，x₂，x₃，x₄的大小关系为：x₁＜x₃＜x₂＜x₄．

点评 本题以导数和函数的极值点为载体，考查了二次函数的图象与性质，所含字母参数较多，属于难题．采用数形结合与分类讨论的思想解题，是本题解决的关键所在．