练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    (1)设函数g(x)＝(x∈R)，且数列{cn}满足c1＝1，cn＝g(cn－1)(n∈N，n＞1)；求数列{cn}的通项公式．

    (2)设等差数列{an}、{bn}的前n项和分别为Sn和Tn，且，，S2＝6；求常数A的值及{an}的通项公式．

    (3)若，其中an、cn即为(1)、(2)中的数列{an}、{cn}的第n项，试求d1＋d2＋…＋dn．

    答案：
    解析：

    　　解：(1)由题意：，变形得：，

    　　∴数列是以为公比，为首项的等比数列．

    　　∴，即．

    　　(2)∵由等差数列、知：；

    　　∴由得：，

    　　∴，∵，∴，解得；

    　　∴，和分别是等差数列、的前n项和；

    　　∴可设；∵，∴，即．

    　　当时，，

    　　当n≥2时，．

    　　综上得：．

    　　(3)当(N*)时，

    　　

    　　

    　　当(N*)时，

    　　

    　　．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    函数f(x)=
    2x
    x2+1
    的定义域为[-
    1
    2
    ，
    1
    2
    ]    ．
    （1）求函数f（x）的值域；
    （2）设函数g(x)=x3-3ax+
    7
    8
    (-
    1
    2
    ≤x≤
    1
    2
    ，且a≥
    1
    4
    )    ．若对于任意x1∈[-
    1
    2
    ，
    1
    2
    ]    ，总存在x2∈[-
    1
    2
    ，
    1
    2
    ]    ，使得g（x2）=f（x1）成立，求a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

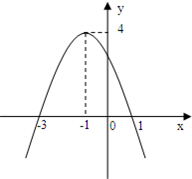    精英家教网如图是一个二次函数y=f（x）的图象
    （1）写出这个二次函数的零点，并求这个二次函数的解析式；
    （2）设函数g(x)=
    f(x)+2xx
    ，判断函数g（x）在区间（0，+∞）上的单调性，并给予证明．

    查看答案和解析>>

    科目：高中数学 来源：云南省2010届高三下学期模拟文科数学试题 人教版 题型：044

    (1)设函数g(x)＝(x∈R)，且数列{cn}满足c1＝1，cn＝g(cn－1)(n∈N，n＞1)；求数列{cn}的通项公式．

    (2)设等差数列{an}、{bn}的前n项和分别为Sn和Tn，且，，S2＝6；求常数A的值及{an}的通项公式．

    (3)若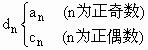，其中an、cn即为(1)、(2)中的数列{an}、{cn}的第n项，试求d1＋d2＋…＋dn．

    查看答案和解析>>

    科目：高中数学 来源：湖北省武汉二中08-09学年高二下学期期末考试（理） 题型：解答题

     定义在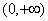的函数, 其中e=2.71828……是自然对数的底数, .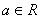

       (1)若函数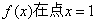处连续, 求a的值；

       (2)若函数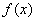为(0, 1)上的单调函数, 求实数a的取值范围, 并判断此时函数 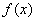在(0, +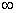)上是否为单调函数；

    (3)当x∈(0,1),设函数g(x)=lnf(x)+x2-ax, 试证明：对时, 有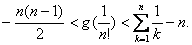

     

     

     

     

     

     

     

    查看答案和解析>>

    同步练习册答案