
【题目】在四边形ABCD中,已知 ![]() ∥
∥ ![]() ,
, ![]() =(6,1),
=(6,1), ![]() =(x,y),
=(x,y), ![]() =(﹣2,﹣3).
=(﹣2,﹣3).
(1)求用x表示y的关系式;
(2)若 ![]() ⊥
⊥ ![]() ,求x、y值.
,求x、y值.
【答案】
(1)解:∵ ![]() =(6,1),
=(6,1), ![]() =(x,y),
=(x,y), ![]() =(﹣2,﹣3),
=(﹣2,﹣3),
∴ ![]()
∵ ![]() ,
,
∴x(﹣2+y)=y(4+x)
∴y=﹣ ![]()
(2)解:∵ ![]() =(6,1),
=(6,1), ![]() =(x,y),
=(x,y), ![]() =(﹣2,﹣3),
=(﹣2,﹣3),
∴ ![]() =(x+6,y+1),
=(x+6,y+1),
![]() =(x﹣2,y﹣3),
=(x﹣2,y﹣3),
∵ ![]() ,
,
∴(x+6)(x﹣2)+(y+1)(y﹣3)=0,
又∵y=﹣ ![]() ,
,
解得 ![]() 或
或 ![]()
【解析】(1) ![]() ,由
,由 ![]() ,能求出y=﹣
,能求出y=﹣ ![]() .(2)
.(2) ![]() =(x+6,y+1),
=(x+6,y+1), ![]() =(x﹣2,y﹣3),由
=(x﹣2,y﹣3),由 ![]() ,y=﹣
,y=﹣ ![]() ,能求出x、y值.
,能求出x、y值.
【考点精析】掌握数量积判断两个平面向量的垂直关系是解答本题的根本,需要知道若平面![]() 的法向量为
的法向量为![]() ,平面
,平面![]() 的法向量为
的法向量为![]() ,要证
,要证![]() ,只需证
,只需证![]() ,即证
,即证![]() ;即:两平面垂直
;即:两平面垂直![]() 两平面的法向量垂直.
两平面的法向量垂直.


科目:高中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为1,P,Q分别为AB,DA上动点,且△APQ的周长为2,设 AP=x,AQ=y. 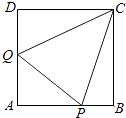
(1)求x,y之间的函数关系式y=f(x);
(2)判断∠PCQ的大小是否为定值?并说明理由;
(3)设△PCQ的面积分别为S,求S的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有甲、乙两种商品,经销这两种商品所能获得的利润分别是p万元和q万元.它们与投入资金x万元的关系是:p= ![]() x,q=
x,q= ![]() .今有3万元资金投入经营这两种商品,为获得最大利润,对这两种商品的资金分别投入多少时,能获取最大利润?最大利润为多少?
.今有3万元资金投入经营这两种商品,为获得最大利润,对这两种商品的资金分别投入多少时,能获取最大利润?最大利润为多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设集合A={x|2﹣5≤2﹣x≤4},B={x|x2+2mx﹣3m2<0,m>0}.
(1)若m=2,求A∩B;
(2)若BA,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数y=f(x)满足以下条件:①定义在正实数集上;②f( ![]() )=2;③对任意实数t,都有f(xt)=tf(x)(x∈R+).
)=2;③对任意实数t,都有f(xt)=tf(x)(x∈R+).
(1)求f(1),f( ![]() )的值;
)的值;
(2)求证:对于任意x,y∈R+ , 都有f(xy)=f(x)+f(y);
(3)若不等式f(loga(x﹣3a)﹣1)﹣f(﹣ ![]()
![]() )≥﹣4对x∈[a+2,a+
)≥﹣4对x∈[a+2,a+ ![]() ]恒成立,求实数a的取值范围.
]恒成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知矩形ABCD的长AB=4,宽AD=3,将其沿对角线BD折起,得到四面体A﹣BCD,如图所示,给出下列结论:
①四面体A﹣BCD体积的最大值为 ![]() ;
;
②四面体A﹣BCD外接球的表面积恒为定值;
③若E、F分别为棱AC、BD的中点,则恒有EF⊥AC且EF⊥BD;
④当二面角A﹣BD﹣C为直二面角时,直线AB、CD所成角的余弦值为 ![]() ;
;
⑤当二面角A﹣BD﹣C的大小为60°时,棱AC的长为 ![]() .
.
其中正确的结论有(请写出所有正确结论的序号).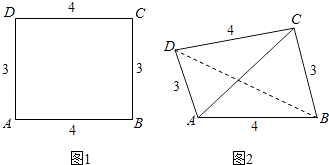
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了迎接青奥会,南京将在主干道统一安装某种新型节能路灯,该路灯由灯柱和支架组成.在如图所示的直角坐标系中,支架ACB是抛物线y2=2x的一部分,灯柱CD经过该抛物线的焦点F且与路面垂直,其中C在抛物线上,B为抛物线的顶点,DH表示道路路面,BF∥DH,A为锥形灯罩的顶,灯罩轴线与抛物线在A处的切线垂直.安装时要求锥形灯罩的顶到灯柱的距离是1.5米,灯罩的轴线正好通过道路路面的中线. 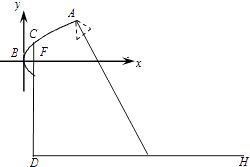
(1)求灯罩轴线所在的直线方程;
(2)若路宽为10米,求灯柱的高.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知直线与抛物线y2=2px(p>0)交于A,B两点,且OA⊥OB,OD⊥AB交AB于点D(不为原点).
(Ⅰ)求点D的轨迹方程;
(Ⅱ)若点D坐标为(2,1),求p的值.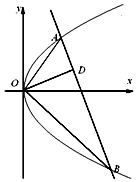
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com