
经销商经销某种农产品,在一个销售季度内,每售出1 t该产品获利润500元,未售出的产品,每1 t亏损300元.根据历史资料,得到销售季度内市场需求量的频率分布直方图,如下图所示.经销商为下一个销售季度购进了130 t该农产品.以X(单位:t,100≤X≤150)表示下一个销售季度内的市场需求量,T(单位:元)表示下一个销售季度内经销该农产品的利润.

(1)将T表示为X的函数;
(2)根据直方图估计利润T不少于57 000元的概率;
(3)在直方图的需求量分组中,以各组的区间中点值代表该组的各个值,并以需求量落入该区间的频率作为需求量取该区间中点值的概率(例如:若需求量X∈[100,110),则取X=105,且X=105的概率等于需求量落入[100,110)的频率),求T的数学期望.
科目:高中数学 来源: 题型:
小王参加一次比赛,比赛共设三关,第一、二关各有两个必答题,如果每关两个问题都答对,可进入下一关,第三关有三个问题,只要答对其中两个问题,则闯关成功.每过一关可一次性获得价值分别为1 000元,3 000元,6 000元的奖品(不重复得奖),小王对三关中每个问题回答正确的概率依次为 ,
, ,
, ,且每个问题回答正确与否相互独立.
,且每个问题回答正确与否相互独立.
(1)求小王过第一关但未过第二关的概率;
(2)用X表示小王所获得奖品的价值,写出X的概率分布列,并求X的数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
曲线C1的参数方程为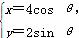 (θ为参数),曲线C2的极坐标方程为ρ=2cos θ-2sin θ.
(θ为参数),曲线C2的极坐标方程为ρ=2cos θ-2sin θ.
(1)化曲线C1,C2的方程为普通方程,并说明它们分别表示什么曲线;
(2)设曲线C1与x轴的一个交点的坐标为P(m,0)(m>0),经过点P作曲线C2的切线l,求切线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
设10≤x1<x2<x3<x4≤104,x5=105.随机变量ξ1取值x1,x2,x3,x4,x5的概率均为0.2,随机变量ξ2取值 的概率也均为0.2.若记Dξ1,Dξ2分别为ξ1,ξ2的方差,则( )
的概率也均为0.2.若记Dξ1,Dξ2分别为ξ1,ξ2的方差,则( )
A.D(ξ1)>D(ξ2)
B.D(ξ1)=D(ξ2)
C.D(ξ1)<D(ξ2)
D.D(ξ1)与D(ξ2)的大小关系与x1,x2,x3,x4的取值有关
查看答案和解析>>
科目:高中数学 来源: 题型:
小波以游戏方式决定是参加学校合唱团还是参加学校排球队.游戏规则为:以O为起点,再从A1,A2,A3,A4,A5,A6,A7,A8(如图)这8个点中任取两点分别为终点得到两个向量,记这两个向量的数量积为X.若X=0就参加学校合唱团,否则就参加学校排球队.
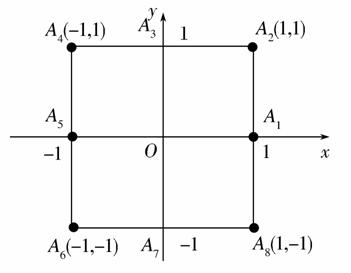
(1)求小波参加学校合唱团的概率;
(2)求X的分布列.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com