
在正方体ABCD-A1B1C1D1中,M、N、P分别是AD1、BD和B1C的中点,

求证:(1)MN∥平面CC1D1D. (2)平面MNP∥平面CC1D1D.
(1)见解析(2)见解析
【解析】
试题分析:
(1)连接AC,CD1 N为BD中点,
 N为AC中点,又 因为M为AD1中点,
N为AC中点,又 因为M为AD1中点,
 MN//CD1
MN//CD1 MN//平面CC1D1D
MN//平面CC1D1D
(2)连接BC1,C1D,B1BCC1为正方形,P为B1C中点,
 P为BC1中点,N为BD中点,
P为BC1中点,N为BD中点, PN// C1D
PN// C1D  PN//平面CC1D1D,
PN//平面CC1D1D,
且MN∩PN=N 平面MNP∥平面CC1D1D.
平面MNP∥平面CC1D1D.
试题解析:
证明:(1)连接AC,CD1,
因为ABCD为正方形,N为BD中点,
所以N为AC中点,
又 因为M为AD1中点,
所以MN//CD1
因为MN¢平面CC1D1D, CD1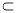 平面CC1D1D,
平面CC1D1D,
所以MN//平面CC1D1D

(2)连接BC1,C1D,
因为B1BCC1为正方形,P为B1C中点,
所以P为BC1中点,
又 因为N为BD中点,
所以PN// C1D
因为PN¢平面CC1D1D, CD1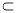 平面CC1D1D,
平面CC1D1D,
所以PN//平面CC1D1D
由(1)知 MN//平面CC1D1D且MN∩PN=N
所以平面MNP∥平面CC1D1D.
考点:线面平行,面面平行.


科目:高中数学 来源:2016届福建省晋江市高一年下学期期中考试数学试卷(解析版) 题型:解答题
设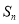 为数列
为数列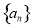 的前
的前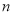 项和,对任意的
项和,对任意的 N,都有
N,都有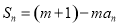
 为常数,且
为常数,且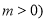 .
.
(1)求证:数列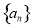 是等比数列;
是等比数列;
(2)设数列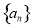 的公比
的公比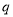 与
与 函数关系为
函数关系为 ,数列
,数列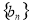 满足
满足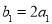 ,点
,点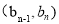 落在
落在  上,
上, ,
, N,求数列
N,求数列 的通项公式;
的通项公式;
(3)在满足(2)的条件下,求数列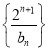 的前
的前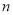 项和
项和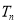 ,使
,使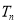
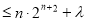 恒成立时,求
恒成立时,求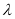 的最小值.[
的最小值.[
查看答案和解析>>
科目:高中数学 来源:2016届福建省厦门市高一3月阶段测试数学试卷(解析版) 题型:选择题
设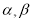 是两个不同的平面,
是两个不同的平面,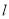 是一条直线,以下命题正确的是( )
是一条直线,以下命题正确的是( )
A.若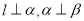 ,则
,则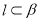 B.若
B.若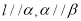 ,则
,则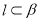
C.若 ,则
,则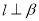 D.若
D.若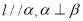 ,则
,则
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com