
设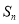 为数列
为数列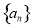 的前
的前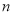 项和,对任意的
项和,对任意的 N,都有
N,都有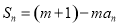
 为常数,且
为常数,且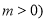 .
.
(1)求证:数列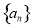 是等比数列;
是等比数列;
(2)设数列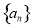 的公比
的公比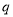 与
与 函数关系为
函数关系为 ,数列
,数列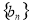 满足
满足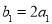 ,点
,点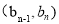 落在
落在  上,
上, ,
, N,求数列
N,求数列 的通项公式;
的通项公式;
(3)在满足(2)的条件下,求数列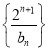 的前
的前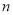 项和
项和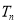 ,使
,使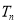
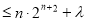 恒成立时,求
恒成立时,求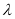 的最小值.[
的最小值.[
(1)证明过程详见试题分析; (2)数列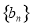 的通项公式为
的通项公式为 ;
;
(3)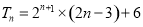 ,
,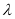 的最小值为-6.
的最小值为-6.
【解析】
试题分析:(1)按照等比数列的定义证明数列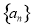 是等比数列;
是等比数列;
(2)由(1)知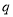 与
与 函数关系为
函数关系为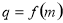
 ,∴
,∴ 是首项为
是首项为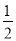 ,公差为1的等差数列,通项公式可求;
,公差为1的等差数列,通项公式可求;
(3)先用错位相减法求出数列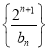 的前
的前 项和
项和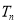 ,即
,即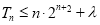 ,化简得
,化简得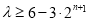 恒成立,由单调性知当
恒成立,由单调性知当 时,右边最大,所以
时,右边最大,所以 ,
, 的最小值为-6.
的最小值为-6.
(1)证明:当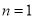 时,
时,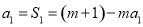 ,解得
,解得 . 1分
. 1分
当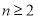 时,
时, . 2分
. 2分
即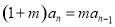 .
.
∵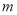 为常数,且
为常数,且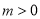 ,∴
,∴
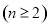 . 3分
. 3分
∴数列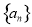 是首项为1,公比为
是首项为1,公比为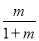 的等比数列. 4分
的等比数列. 4分
(2)【解析】
由(1)得,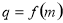
 ,
, . 5分
. 5分
∵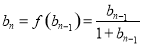
∴ ,即
,即
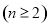 .
.
∴ 是首项为
是首项为 ,公差为1的等差数列. 7分
,公差为1的等差数列. 7分
∴ ,即
,即 (
(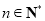 ). 8分
). 8分
(3)【解析】
由(2)知 ,则
,则 . 9分
. 9分
所以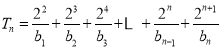 ,
,
即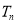
 , ①
, ①
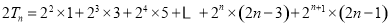 , ②
, ②
②-①得 ,
,
故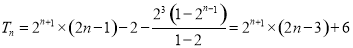 .
.
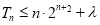 ,化简得
,化简得 恒成立,由单调性知当
恒成立,由单调性知当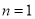 时,右边最大,所以
时,右边最大,所以 ,
, 的最小值为-6. 14分
的最小值为-6. 14分
考点:数列综合应用、函数与方程思想、恒成立问题.


 发散思维新课堂系列答案
发散思维新课堂系列答案科目:高中数学 来源:2016届福建省高一下学期第一阶段考试数学试卷(解析版) 题型:选择题
将边长为a的正方形ABCD沿对角线AC折起,使BD=a,则三棱锥D—ABC的体积为( )
A.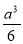 B.
B.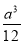 C.
C. D.
D.
查看答案和解析>>
科目:高中数学 来源:2016届福建省晋江市高一年下学期期中考试数学试卷(解析版) 题型:选择题
为测树的高度,在水平地面上选取A、B两点(点A、B及树的底部在同一直线上),从A、B两点分别测得树尖的仰角为30°,45°,且A、B两点间的距离为60m,则树的高度为( )
A. B.
B.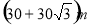
C.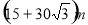 D.
D.
查看答案和解析>>
科目:高中数学 来源:2016届福建省厦门市高一3月阶段测试数学试卷(解析版) 题型:解答题
在正方体ABCD-A1B1C1D1中,M、N、P分别是AD1、BD和B1C的中点,

求证:(1)MN∥平面CC1D1D. (2)平面MNP∥平面CC1D1D.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com