练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】某同学在研究函数时，给出下面几个结论中正确的有( )

    A.的图象关于点对称B.若，则

    C.的值域为D.函数有三个零点

    【答案】BC

    【解析】

    先判断函数的奇偶性，再利用绝对值性质化简函数的解析式，判断函数的值域，然后再根据零点的定义判断即可.

    函数的定义域为全体实数，，所以是奇函数，图象关于原点对称，.

    选项A：由上分析函数关于原点对称，若函数关于对称，原点关于对称的点是，而，显然不在该图象上，故函数不关于对称，本选项是错误的；

    选项B：当时，，显然函数单调递增，此时；

    当时，，显然函数单调递增，此时，因此函数在整个实数集上是单调递增的，因此若，则是正确的，本选项是正确的；

    选项C：由选项B的分析可以知道本选项是正确的；

    选项D：，只有一个零点，故本选项是错误的.

    故选：BC

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知椭圆的左右焦点与其短轴的一个端点是正三角形的三个顶点，点在椭圆上，直线与椭圆交于，两点，与轴、轴分别相交于点和点，且，点是点关于轴的对称点，的延长线交椭圆于点，过点、分别做轴的垂线，垂足分别为、.

    （1）求椭圆的方程；

    （2）是否存在直线，使得点平分线段，？若存在，求出直线的方程；若不存在，请说明理由.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】将函数图象上所有点的横坐标缩短为原来的，纵坐标不变，再向右平移个单位长度，得到函数的图象，则下列说法正确的是（ ）

    A. 函数的一条对称轴是

    B. 函数的一个对称中心是

    C. 函数的一条对称轴是

    D. 函数的一个对称中心是

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数，其中．

    （1）求函数的单调区间；

    （2）若函数存在两个极值点，，且，证明：．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图所示, 是边长为3的正方形, 平面与平面所成角为.

    (Ⅰ)求证： 平面；

    (Ⅱ)设点是线段上一个动点,试确定点的位置,使得平面,并证明你的结论．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知实数，定义域为的函数是偶函数，其中为自然对数的底数．

    （Ⅰ）求实数值；

    （Ⅱ）判断该函数在上的单调性并用定义证明；

    （Ⅲ）是否存在实数，使得对任意的，不等式恒成立．若存在，求出实数的取值范围；若不存在，请说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】下面是一幅统计图，根据此图得到的以下说法中正确的是（ ）

    A.这几年生活水平逐年得到提高

    B.生活费收入指数增长最快的一年是2015年

    C.生活价格指数上涨速度最快的一年是2016年

    D.虽然2017年的生活费收入增长缓慢，但生活价格指数略有降低，因而生活水平有较大的改善

    E.2016年生活价格指数上涨的速度与2017年生活价格指数下降的速度相同

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某厂推出品牌为“玉兔”的新产品，生产“玉兔”的固定成本为20000元，每生产一件“玉兔”需要增加投入100元，根据统计数据，总收益P（单位：元）与月产量x（单位：件）满足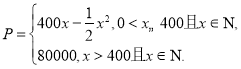（注：总收益=总成本+利润）

    （1）请将利润y（单位：元）表示成关于月产量x（单位：件）的函数；

    （2）当月产量为多少时，利润最大？最大利润是多少？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】下列关于回归分析与独立性检验的说法正确的是（）

    A.回归分析和独立性检验没有什么区别；

    B.回归分析是对两个变量准确关系的分析，而独立性检验是分析两个变量之间的不确定性关系；

    C.独立性检验可以确定两个变量之间是否具有某种关系．

    D.回归分析研究两个变量之间的相关关系，独立性检验是对两个变量是否具有某种关系的一种检验；

    查看答案和解析>>

    同步练习册答案