练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】为得到函数y=cos（x+ ）的图象，只需将函数y=sinx的图象（ ）
    A.向左平移 个长度单位
    B.向右平移 个长度单位
    C.向左平移 个长度单位
    D.向右平移 个长度单位

    【答案】C
    【解析】解：∵y=cos（x+ ）

    =cos（﹣x﹣ ）

    =sin[ ﹣（﹣x﹣ ）]

    =sin（x+ ），

    ∴要得到y=sin（x+ ）的图象，只需将函数y=sinx的图象向左平移 个长度单位，

    故选C．

    【考点精析】解答此题的关键在于理解函数y=Asin（ωx+φ）的图象变换的相关知识，掌握图象上所有点向左（右）平移个单位长度，得到函数的图象；再将函数的图象上所有点的横坐标伸长（缩短）到原来的倍（纵坐标不变），得到函数的图象；再将函数的图象上所有点的纵坐标伸长（缩短）到原来的倍（横坐标不变），得到函数的图象．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知矩形ABCD（AB＞AD）的周长为12，若将它关于对角线AC折起后，使边AB与CD交于点P（如图所示），则△ADP面积的最大值为 ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）=cos2x的图象向左平移 个单位后得到函数g（x）的图象，若使|f（x1）﹣g（x2）|=2成立x1 ， x2的满足 ，则φ的值为（ ）
    A.
    B.
    C.
    D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】阅读如图程序框图，运行相应的程序，则程序运行后输出的结果为（ ）
    A.7
    B.9
    C.10
    D.11

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设关于x的一元二次方程x2+ax﹣ +1=0．
    （1）若a是从1，2，3这三个数中任取的一个数，b是从0，1，2这三个数中任取的一个数，求上述方程中有实根的概率；
    （2）若a是从区间[0，3]中任取的一个数，b是从区间[0，2]中任取的一个数，求上述方程有实根的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆C： ，F1 ， F2分别为左右焦点，在椭圆C上满足条件 的点A有且只有两个
    （1）求椭圆C的方程
    （2）若过点F2的两条相互垂直的直线l1与l2 ， 直线l1与曲线y2=4x交于两点M、N，直线l2与椭圆C交于两点P、Q，求四边形PMQN面积的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】定义在R上的连续函数f（x）满足f（1）=2，且f（x）在R上的导函数f′（x）＜1，则不等式f（x）＜x+1的解集为 ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在四棱锥P﹣ABCD中，PD⊥平面ABCD，底面ABCD为菱形，E为棱PB的中点，O为AC与BD的交点，
    （Ⅰ）证明：PD∥平面EAC
    （Ⅱ）证明：平面EAC⊥平面PBD．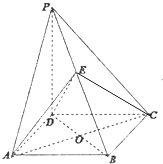

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知 =（1，2）， =（﹣3，2）， 当k=时，（1）k + 与 ﹣3 垂直；
    当k=时，（2）k + 与 ﹣3 平行．

    查看答案和解析>>

    同步练习册答案