
分析 (1)化简集合A=[-1,4],B=[m-3,m+3],从而可得$\left\{\begin{array}{l}{m-3=0}\\{m+3≥4}\end{array}\right.$,从而解得;
(2)化简C={y|y=ax+b,a>0,且a≠1,x∈R}=(b,+∞),从而解得.
解答 解:(1)A={x|x2-3x-4≤0}=[-1,4],
B={x|x2-2mx+m2-9≤0}=[m-3,m+3],
∵A∩B=[0,4],
∴$\left\{\begin{array}{l}{m-3=0}\\{m+3≥4}\end{array}\right.$,
解得,m=3;
(2)C={y|y=ax+b,a>0,且a≠1,x∈R}
=(b,+∞),
∵A∩C只有一个子集,
∴A∩C=∅,
∴b≥4.
点评 本题考查了集合的化简与运算,同时考查了不等式的解法.


 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{1}{4}$ | B. | -$\frac{1}{8}$ | C. | -$\frac{\sqrt{3}}{8}$ | D. | -$\frac{3}{16}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{5π}{6}$ | B. | $\frac{2π}{3}$ | C. | $\frac{π}{3}$ | D. | $\frac{π}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {1,2,3} | B. | {1,3,4} | C. | {1,4,5} | D. | {2,3,5} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
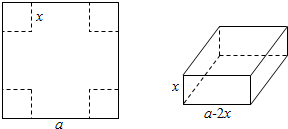 有一块边长为a的正方形铁板,现从铁板的四个角各截去一个相同的小正方形,做成一个长方体形的无盖容器,为使其容积最大,截下的小正方形边长应为多少?
有一块边长为a的正方形铁板,现从铁板的四个角各截去一个相同的小正方形,做成一个长方体形的无盖容器,为使其容积最大,截下的小正方形边长应为多少?查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com