
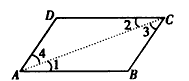
证明:(1)连接AC;
(2)平面几何中的三角形“边边边”定理有:有三边对应相等的两个三角形全等,这一定理相当于: 对于任意两个三角形,如果它们的三边对应相等,则这两个三角形全等, 大前提;
△ABC和△CDA的三边对应相等,小前提;
则这两个三角形全等,结论;
符号表示: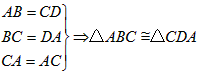 ;
;
(3)由全等三角形的定义可知:全等三角形的对应角相等,这一性质相当于:对于任意两个三角形,如果它们全等,则它们的对应角相等,大前提;
△ABC和△CDA全等,小前提;
则它们的对应角相等,结论;
用符号表示,就是△ABC≌△CDA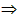 ∠1=∠2且∠3=∠4 且∠B=∠D;
∠1=∠2且∠3=∠4 且∠B=∠D;
(4)两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行,大前提;
直线AB、DC被直线AC所截,内错角∠1=∠2,小前提;
则AB∥DC,结论;
同理有:BC∥AD;
(5)如果四边形两组对边分别平行,那么这个四边形是平行四边形,大前提;
四边形ABCD中,两组对边分别平行,小前提;
则四边形ABCD是平行四边形,结论;
用符号表示为:AB∥DC且AD∥BC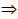 四边形ABCD为平行四边形。
四边形ABCD为平行四边形。


科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com