练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    如下图，已知P是平行四边形ABCD所在平面外一点，M、N分别是AB、PC的中点．

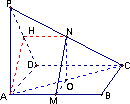
    (1)求证：MN∥平面PAD；

    (2)若MN＝BC＝4，，求异面直线PA与MN所成角的大小．

    答案：
    解析：

    　　略证(1)：取PD的中点H，连接AH，

    　　

    　　为平行四边形

    　　

    　　解(2)：连接AC并取其中点为O，连接OM、ON，则OM平行且等于BC的一半，ON平行且等于PA的一半，所以就是异面直线与所成的角，由，得，OM＝2，ON＝．

    　　所以，即异面直线与成的角．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：吉林省长春外国语学校2011－2012学年高二第一次月考数学试题 题型：047

    如下图所示，已知P是平行四边形ABCD所在平面外一点，M、N分别是AB、PC的中点，平面PAD平面PBC＝l．

    (1)求证：l∥BC；

    (2)MN与平面PAD是否平行？试证明你的结论．

    查看答案和解析>>

    科目：高中数学 来源：全优设计选修数学－2-1苏教版 苏教版 题型：047

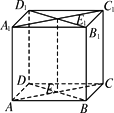
    如下图中，已知点O是平行六面体ABCD－A1B1C1D1体对角线的交点，点P是任意一点，则＋＋＋＋＋＋＋＝8．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

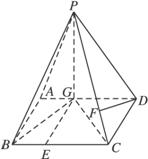
    如下图，已知四棱锥P-ABCD中，底面ABCD是平行四边形，PG⊥平面ABCD，垂足为G，G在AD上，且AG=GD，BG⊥GC，GB=GC=2，四面体P-BCG的体积为.

    （1）求点D到平面PBG的距离；

    （2）若F点是棱PC上一点，且DF⊥GC，求的值.

    查看答案和解析>>

    同步练习册答案