
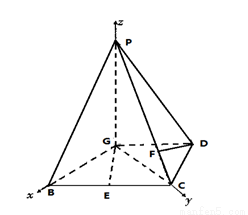
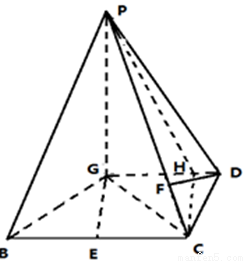
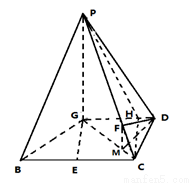
已知四棱锥P—GBCD中(如图),PG⊥平面GBCD,GD∥BC,GD=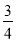 BC,且BG⊥GC,GB=GC=2,E是BC的中点,PG=4
BC,且BG⊥GC,GB=GC=2,E是BC的中点,PG=4
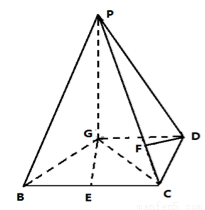
(1)求异面直线GE与PC所成角的余弦值;
(2)若F点是棱PC上一点,且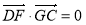 ,
,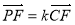 ,求
,求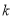 的值.
的值.
(1)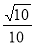 ,(2)
,(2)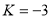
【解析】
试题分析:法一:空间向量法。(1)以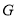 为坐标原点,以
为坐标原点,以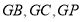 所在直线分别为
所在直线分别为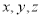 轴建立空间直角坐标系。根据已知条件得点的坐标,再得向量的坐标。用向量数量积公式求向量
轴建立空间直角坐标系。根据已知条件得点的坐标,再得向量的坐标。用向量数量积公式求向量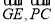 所成角的余弦值,但应注意空间两异面直线所成的角为锐角或直角,所以两异面
所成角的余弦值,但应注意空间两异面直线所成的角为锐角或直角,所以两异面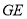 和
和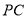 所成角的余弦值为向量
所成角的余弦值为向量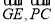 所成角的余弦值的绝对值。(2)根据题意设
所成角的余弦值的绝对值。(2)根据题意设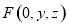 ,根据
,根据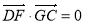 ,可得
,可得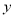 的值,根据比例关系即可求得
的值,根据比例关系即可求得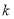 的值。法二:普通方法。(1)根据异面直线所成角的定义可过
的值。法二:普通方法。(1)根据异面直线所成角的定义可过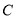 点作
点作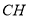 //
//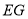 交
交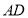 于
于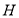 ,则
,则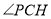 (或其补角)就是异面直线
(或其补角)就是异面直线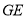 与
与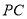 所成的角. 因为
所成的角. 因为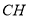 //
//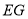 且
且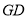 //
//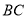 ,则四边形
,则四边形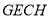 为平行四边形,则
为平行四边形,则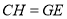 ,
,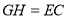 ,故可在
,故可在 中用余弦定理求
中用余弦定理求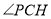 。(2)由
。(2)由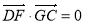 可得
可得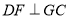 ,过
,过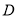 作
作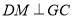 ,
,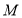 为垂足。易得证
为垂足。易得证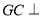 平面
平面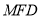 ,可得
,可得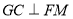 ,从而易得证
,从而易得证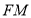 //
//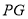 ,可得
,可得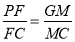 ,即可求
,即可求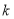 的值。
的值。
试题解析:解法一:
(1)如图所示,以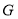 点为原点建立空间直角坐标系
点为原点建立空间直角坐标系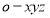 ,
,
则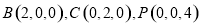 故
故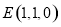
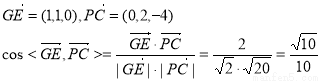
故异面直线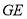 与
与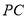 所成角的余弦值为
所成角的余弦值为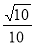 .
.
(2)设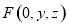
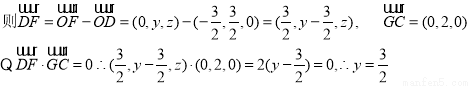
在平面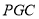 内过
内过 点作
点作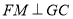 ,
,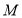 为垂足,则
为垂足,则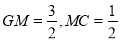
 ,∴
,∴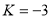
解法二:
(1)在平面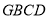 内,过
内,过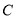 点作
点作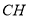 //
//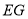 交
交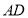 于
于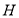 ,连结
,连结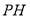 ,则
,则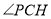 (或其补角)就是异面直线
(或其补角)就是异面直线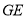 与
与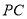 所成的角.
所成的角.
在 中,
中,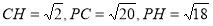
由余弦定理得,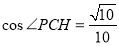
∴异面直线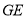 与
与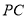 所成角的余弦值为
所成角的余弦值为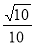 .
.
(2)在平面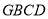 内,过
内,过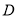 作
作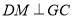 ,
,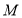 为垂足,连结
为垂足,连结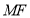 ,又因为
,又因为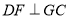
∴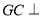 平面
平面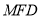 ,
, ∴
∴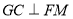
由平面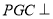 平面
平面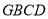 ,∴
,∴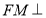 平面
平面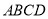 ∴
∴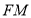 //
//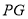
由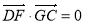 得
得 ,∴
,∴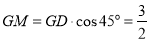
 ,∴
,∴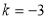 .
.
考点:1异面直线所成的角;2线线垂直、线面垂直、面面垂直;3空间向量法解立体几何问题。


 快乐5加2金卷系列答案
快乐5加2金卷系列答案科目:高中数学 来源:2013-2014学年湖北省七市(州)高三年级联合考试理科数学试卷(解析版) 题型:选择题
下列说法错误的是( )
A.命题“若x2-5x+6=0,则x=2”的逆否命题是“若x≠2,则x2-5x+6≠0”
B.已知命题p和q,若p∨q为假命题,则命题p与q中必一真一假
C.若x,y∈R,则“x=y”是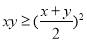 的充要条件
的充要条件
D.若命题p: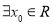 ,
,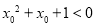 则
则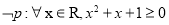
查看答案和解析>>
科目:高中数学 来源:2013-2014学年浙江省高三高考模拟冲刺卷(提优卷)(二)理科数学试卷(解析版) 题型:选择题
李先生居住在城镇的A处,准备开车到单位B处上班,途中(不绕行)共要经过6个交叉路口,假设每个交叉路口发生堵车事件的概率均为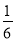 ,则李先生在一次上班途中会遇到堵车次数
,则李先生在一次上班途中会遇到堵车次数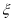 的期望值
的期望值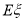 是( )
是( )
A.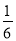 B.1 C.
B.1 C.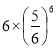 D.
D.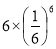
查看答案和解析>>
科目:高中数学 来源:2013-2014学年浙江省高三高考模拟冲刺卷(提优卷)(二)文科数学试卷(解析版) 题型:选择题
正四面体ABCD的棱长为1,其中线段AB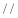 平面
平面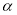 ,E,F分别是线段AD和BC的中点,当正四面体绕以AB为轴旋转时,线段EF在平面
,E,F分别是线段AD和BC的中点,当正四面体绕以AB为轴旋转时,线段EF在平面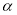 上的射影
上的射影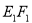 长的范围是( )
长的范围是( )
A.[0,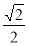 ] B.[
] B.[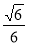 ,
,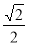 ]
]
C.[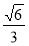 ,
,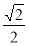 ] D.[
] D.[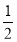 ,
,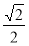 ]
]
查看答案和解析>>
科目:高中数学 来源:2013-2014学年浙江省高三高考模拟冲刺卷(提优卷)(二)文科数学试卷(解析版) 题型:选择题
设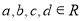 ,则“
,则“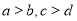 ”是“
”是“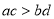 ”成立的 ( )
”成立的 ( )
A.充分不必要条件 B.必要不充分条件
C.充分必要条件 D.既不充分也不必要条件
查看答案和解析>>
科目:高中数学 来源:2013-2014学年浙江省高三高考模拟冲刺卷(提优卷)(三)理科数学试卷(解析版) 题型:填空题
已知定义在R上的函数f(x),g(x)满足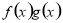 =ax,且f′(x)g(x)+f(x)·g′(x)<0,
=ax,且f′(x)g(x)+f(x)·g′(x)<0,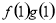 +
+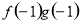 =
=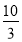 ,若有穷数列{
,若有穷数列{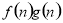 }(n∈N*)的前n项和等于
}(n∈N*)的前n项和等于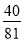 ,则n等于 .
,则n等于 .
查看答案和解析>>
科目:高中数学 来源:2013-2014学年浙江省高三高考模拟冲刺卷(提优卷)(三)文科数学试卷(解析版) 题型:填空题
在△ABC中,角A,B,C的对边分别为a,b,c,已知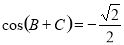 ,
,
bsin=a+ csin,则C= .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com